Return to Other Sample Exams.
Math 223 Name
Fall 1997
Test 1
Directions: Please read each question carefully and show all your work
in doing each question. No partial credit will be given if you do not
show your work. If you have any questions about the test, please ask me.
Your work should of course be your own. Good Luck!
- 1.
- (5 points) Consider the function z = f(x,y) given by
the table below. Determine whether or not the function is linear and
explain your reasoning.
x  y y |
-2 |
|
2 |
|
| -2 |
6 |
3 |
|
|
| |
4 |
1 |
-2 |
|
| 2 |
2 |
-1 |
|
|
- 2.
- (10 points) Consider the surface given by
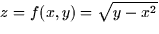 . Make a contour plot showing
contours for z = 0,1,2,3.
. Make a contour plot showing
contours for z = 0,1,2,3.
- 3.
- (20 points) Consider the vector
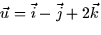 .
.
- (a)
- Find a unit vector in the direction of
 .
.
- (b)
- Find a nonzero vector
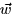 such that
such that 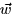 is perpendicular to
is perpendicular to  .
. - (c)
- Given the vector
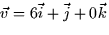 ,find the component of
,find the component of 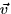 parallel to
parallel to  .
.
- 4.
- (20 points) You are given vectors
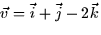 and
and
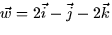 . Let
. Let 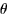 be the smallest angle between
be the smallest angle between 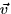 and
and 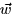 .
.
- (a)
- Use the definitions of the dot product to find
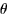 .
. - (b)
- Use the definitions of the cross product to find
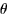 .
.
- 5.
- (20 points) Find an equation of the plane containing the points
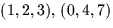 and (-1,6,1).
and (-1,6,1).
- 6.
- (15 points)
Consider the surface z = f(x,y) above.
- (a)
- Sketch a cross-section of the surface with x = 2.
- (b)
- Is fx(1,2.5) positive or negative? Explain your reasoning.
- (c)
- Is fx(1,2.5) larger or smaller than fy(3,0.75)?
Explain your reasoning.
- 7.
- (10 points) Consider
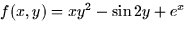 .
.
- (a)
- Find
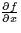 .
. - (b)
- Find
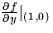 .
.
Vector Calculus
8/21/1998
 .
.
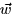 such that
such that 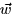 is perpendicular to
is perpendicular to  .
.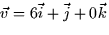 ,find the component of
,find the component of 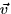 parallel to
parallel to  .
.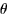 .
.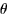 .
.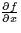 .
.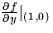 .
.