Return to Other Sample Exams.
Math 223 Name
Fall 1998
Test 1
Directions: Please read each question carefully and show all your work
in doing each question. No partial credit will be given if you do not
show your work. If you have any questions about the test, please ask me.
Your work should of course be your own. Good Luck!
- 1.
- (5 points) Consider the function z = f(x,y) given by
the table below. Determine whether or not the function is linear and
explain your reasoning.
x 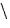 y y |
-2 |
0 |
2 |
| -2 |
4 |
2 |
1 |
| 0 |
3 |
1 |
0 |
| 2 |
2 |
0 |
-1 |
- 2.
- (10 points) Consider the surface given by
z = f(x,y) = 2x - y2. Make a contour plot showing
contours for z = -1,0,1,2.
- 3.
- (20 points) Consider the plane given by z = 1 + x - 2y
and the point Q = (1,2,3). In this problem you will compute
the shortest distance from the point Q to the plane.
- (a)
- Find any point, P, on the plane and write the displacement
vector
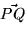 in components.
in components.
- (b)
- Find a unit normal vector to the plane.
- (c)
- Find the component of
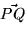 parallel to the unit
normal vector you found above, i.e. find
parallel to the unit
normal vector you found above, i.e. find 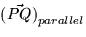 .
. - (d)
- Find the length of
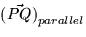 .
.
- 4.
- (20 points) You are given vectors
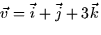 and
and
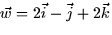 . Let
. Let 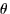 be the smallest angle between
be the smallest angle between 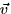 and
and 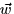 .
.
- (a)
- Use the definitions of the dot product to find
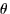 .
. - (b)
- Use the definitions of the cross product to find
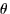 .
.
Note: You should have discovered in part (a) that
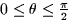 .
.
- 5.
- (20 points) Find an equation of the plane containing the points
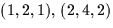 and (-1,-2,5).
and (-1,-2,5).
- 6.
- (15 points)
Consider the surface z = f(x,y) above.
- (a)
- Sketch a cross-section of the surface with x = 1.5.
- (b)
- Is fx(1,1) positive or negative? Explain your reasoning.
- (c)
- Is fx(1,1) greater than or less than fy(1.5,1.5)?
Explain your reasoning.
- 7.
- (10 points) Consider
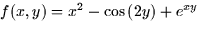 .
.
- (a)
- Find
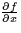 .
. - (b)
- Find
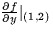 .
.
Vector Calculus
10/13/1998
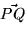 in components.
in components.
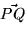 parallel to the unit
normal vector you found above, i.e. find
parallel to the unit
normal vector you found above, i.e. find 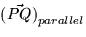 .
.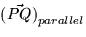 .
.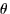 .
.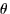 .
. 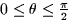 .
.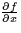 .
.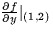 .
.