- (a)
- Whish of the following functions could not have a single
global maximum?
a. 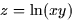
b. 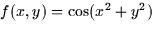
c. 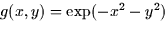
d. z = x2 + 2xy + y2 - (b)
- If
 , which of the following are possible
values for the directional derivative of f in the direction making an
angle
, which of the following are possible
values for the directional derivative of f in the direction making an
angle 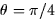 with the x-axis at the point (2,1)?
with the x-axis at the point (2,1)?
I. 0 II. 4 III. -2 a. I only b. II only c. II and III d. I and III - (c)
- Suppose at some point a function f has
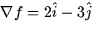 . The rate of maximum decrease of f at this point is in the
direction of the vector:
. The rate of maximum decrease of f at this point is in the
direction of the vector:
a. 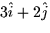
b. 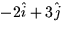
c. 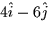
d. along a vector perpendicular to 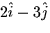
- (d)
- At the point (-1,2) on the graph of z = f(x,y) we know that
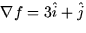 , fxx = -2 and the discrimminant, D = 1.
Thus the point (-1,2) is
, fxx = -2 and the discrimminant, D = 1.
Thus the point (-1,2) is
a. a local maximum b. a local minimum c. a saddle point d. not a critical point
- (a)
- Find the first partial derivatives of f.
- (b)
- Find all the second partial derivatives of f.
- (c)
- Find the normal vector to the surface z = f(x,y) at the point (-1,1,0).
g(x,y) = x2 - 8x + 2y2 + 19
on the disk- (a)
- Write an expression for the volume in terms of w, l, h. Solve this expression for h.
- (b)
- Now suppose that it costs 1 cent/square cm for the material on the sides of the box and 2 cents/square cm for the material forming the tops and bottom. Let C(w,l,h) represent the total cost of the box. Find an expression for C. Drawing a picture may help.
- (c)
- Substitute the expression for h from part (a) into C. Now set up, but do not solve the algebraic equations to find the dimensions of the box that minimize the total cost of the box.