Return to Other Sample Exams.
SECOND HOUR EXAM
MATH 223
Instructor: Kris Green
March 6, 1998
9:00-9:50
Note: This exam covers 13, 14, 20.1 and 20.3
- 1.
- The following questions pertain to vector fields.
- (a)
- Write down the formula for a nonzero vector field that has zero
divergence and is curl free.
- (b)
- Find div
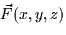 at the point (1,-1,3) if
at the point (1,-1,3) if 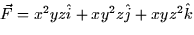 .
. - (c)
- Compute the curl of
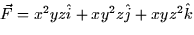 .
.
- 2.
- Find and classify all of the critical points of the function
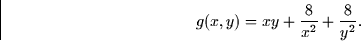
- 3.
- The depth of a pond with coordinates (x,y) is given by
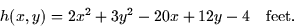
- (a)
- If a boat is at (2,1) and moving in the direction of the vector
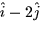 ,is the water getting deeper or shallower? At what rate? Assume that x
and y are measured in feet.
,is the water getting deeper or shallower? At what rate? Assume that x
and y are measured in feet.
- (b)
- In which direction should the boat move at (2,1) in order for the
depth to remain constant? Give a unit vector, not a general description.
- (c)
- At what point is the water the deepest? What is the depth here?
- 4.
-
- (a)
- The vector field below represents the gradient vector field of the
function f(x,y). Draw the location of all extrema on the graph and
sketch two of the level curves. Identify each of the extrema as a local
maximum, minimum, or saddle point.
- (b)
- The vector field grad f(x,y) is shown below again. Suppose we wish
to maximize the value of f(x,y) subject to the constraint g(x,y) = c,
which is also shown.
Label the points on the graph where this maximum value could occur.
- 5.
- The quantity z can be expressed as a function of x and y as z
= f(x,y). Now x and y are also functions of u and v so that x =
g(u,v) and y = h(u,v).
- (a)
- Write dz/du and dz/dv using the chain rule.
- (b)
- Suppose that when
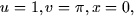 and y = -1. In
addition, you know that
and y = -1. In
addition, you know that 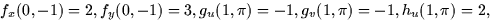 and
and 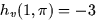 . What are
. What are
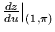 and
and 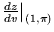 ?
?
- (c)
- Now suppose that u and v are functions of t so that when u =
1 and
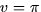 we have du/dt = 3 and dv/dt = 2. What is dz/dt at
this point?
we have du/dt = 3 and dv/dt = 2. What is dz/dt at
this point?
- (d)
- Furthermore, you know that f(0,-1) = 7. What is the equation of
the tangent plane to f(x,y) at this point?
Vector Calculus
8/20/1998
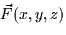 at the point (1,-1,3) if
at the point (1,-1,3) if 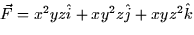 .
.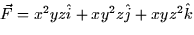 .
.![]()
![]()
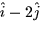 ,is the water getting deeper or shallower? At what rate? Assume that x
and y are measured in feet.
,is the water getting deeper or shallower? At what rate? Assume that x
and y are measured in feet.


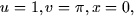 and y = -1. In
addition, you know that
and y = -1. In
addition, you know that 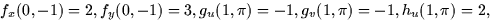 and
and 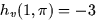 . What are
. What are
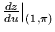 and
and 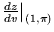 ?
?
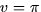 we have du/dt = 3 and dv/dt = 2. What is dz/dt at
this point?
we have du/dt = 3 and dv/dt = 2. What is dz/dt at
this point?