Return to Other Sample Exams.
SECOND HOUR MAKEUP EXAM
MATH 223
Instructor: Kris Green
March 9, 1998
10:00-10:50
Note: This covers 13, 14, 20.1 and 20.3
- 1.
- For the function
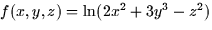
- (a)
- Find a vector pointing in the direction of the maximum rate of change
of f at the point (1, -1, 3).
- (b)
- Let
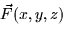 represent the gradient vector field of
f(x,y,z) given above. What is div
represent the gradient vector field of
f(x,y,z) given above. What is div 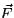 at the point (1,
-1, 3)?
at the point (1,
-1, 3)?
- (c)
- What is curl
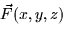 ?
?
- 2.
- Find and classify all of the critical points of the function
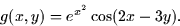
(Hint: Solve for y in terms of x in the second equation that you find.
Then, plug this into the first equation.)
- 3.
- A hiker is climbing a mountain which can be described by the function
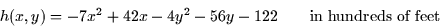
where x and y represent the distance east and north (in feet),
respectively, from the hiker's parked car.
- (a)
- Starting at the car, in which direction (a vector) should the hiker
walk in order to get to a higher altitude as quickly as possible?
- (b)
- Where is the peak of the mountain located with respect to the car?
What is the elevation of this peak?
- (c)
- A short while after leaving the car, the hiker is at the point (-1,
5). If the hiker walks toward the peak, will the elevation be increasing or
decreasing? At what rate?
- (d)
- If the hiker is at the point (-1,5) and wishes to walk without
climbing any higher or dropping any lower, in which direction should he/she
walk?
- 4.
-
- (a)
- The vector field below represents the gradient vector field of the
function f(x,y). Draw the location of all extrema on the graph and
sketch two of the level curves. Identify each of the extrema as a local
maximum, minimum, or saddle point.
- (b)
- The vector field grad f(x,y) is shown below again. Suppose we wish
to maximize the value of f(x,y) subject to the constraint g(x,y) = c,
which is also shown.
Label the points on the graph where this maximum value could occur.
- 5.
- The quantity z can be expressed as a function of x and y as z
= f(x,y). Now x and y are also functions of u and v so that x =
g(u,v) and y = h(u,v).
- (a)
- Write dz/du and dz/dv using the chain rule.
- (b)
- Suppose that when
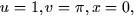 and y = -1. In
addition, you know that
and y = -1. In
addition, you know that 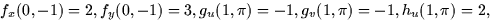 and
and 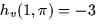 . What are
. What are
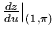 and
and 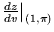 ?
?
- (c)
- Now suppose that u and v are functions of t so that when u =
1 and
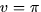 we have du/dt = 3 and dv/dt = 2. What is dz/dt at
this point?
we have du/dt = 3 and dv/dt = 2. What is dz/dt at
this point?
- (d)
- Furthermore, you know that f(0,-1) = 7. What is the equation of
the tangent plane to f(x,y) at this point?
Vector Calculus
8/20/1998
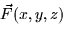 represent the gradient vector field of
f(x,y,z) given above. What is div
represent the gradient vector field of
f(x,y,z) given above. What is div 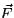 at the point (1,
-1, 3)?
at the point (1,
-1, 3)?
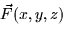 ?
?
![]()
![]()


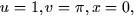 and y = -1. In
addition, you know that
and y = -1. In
addition, you know that 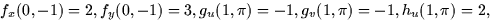 and
and 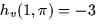 . What are
. What are
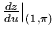 and
and 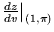 ?
?
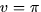 we have du/dt = 3 and dv/dt = 2. What is dz/dt at
this point?
we have du/dt = 3 and dv/dt = 2. What is dz/dt at
this point?