- (a)
- Find
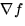 .
. - (b)
- Find the directional derivative of f at the point P = (3,1)
in the direction of
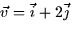 .
. - (c)
- Give a vector in the direction of the most negative directional
derivative at the point
P = (3,1). - (d)
- Give a vector in the direction of zero directional derivative at the point P = (3,1).
- (e)
- Consider the points P = (3,1) and Q = (5,-1). Would you expect the contours of f to be closer together at P than they are at Q? Why or why not?
=3ingraph7.ps
- (a)
- Consider the graph of the surface z = f(x,y) shown above. In the space provided, draw the coordinate axes for the xy-plane and then draw a vector in the direction of the gradient of f(,x,y) at the point P = (0.5,0.5).
- (b)
- Is the magnitude of the gradient larger at P = (0.5,0.5) or Q = (1,1)? Explain your reasoning.
- (c)
- Would you expect
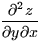 to
be positive or negative at R = (1,0.5)? Explain your reasoning.
to
be positive or negative at R = (1,0.5)? Explain your reasoning.
z = f(x,y) = e(x<<53>>2-y).
Hint: The integral may not be easy to evaluate in the form given.
- (a)
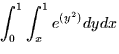 .
.- (b)
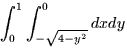 .
.