- (a)
- The determinant of the Jacobian for the change of coordinates x =
-u2, y = u-v+w, z = u-v-w is
a. 0 b. 4 c. -4u d. 4 u - (b)
- Given the line parameterized by x = 2t - 1, y = 3 - (5/3)t,
z=2, a vector pointing in the direction of the line is
a. 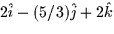
b. 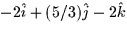
c. 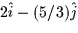
d. 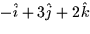
- (c)
- The plane passing through the point (-1,3,2) containing the vectors
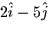 and
and 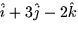 is parameterized
by:
is parameterized
by:
a. x = -1 + 2p + q, y=3-5p + 3q, z = 2-2q b. x = -1 + 3p, y = 3 + 2p, z = 2- 2p c. x = 1 - p +2q, y = 3 + 3p - 5q, z = -2 + 2p d. x = -1 + p +2q, y = 3 + 3p - 5q, z = 2 - 2q - (d)
- The curve
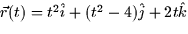 intersects the sphere x2 + y2 + z2 = 16 at time:
intersects the sphere x2 + y2 + z2 = 16 at time:
a. t = 0 b. t = 1 c. the points 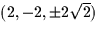
d. both (a) and (c) e. both (a) and (b)
![]()
![]()
- (a)
- Sketch the orbit of Qix.
- (b)
- As seen from the planet, write the parametric equations for the motion of the moon around Qix.
- (c)
- Now, place the origin of your coordinates at Caleb II and use vector addition to help you write the parametric equations for the motion of the moon around the star.
- (d)
- EXTRA CREDIT (5 points):
- i.
- How many days does it take Qix to complete an orbit? (ie. how long is a year on Qix?)
- ii.
- How many times does the moon orbit Qix in one year?
![]()
- (a)
- Find the speed of the Flaming Dragon as a function of time.
- (b)
- Find the acceleration of the Flaming Dragon as a function of time.
- (c)
- How far does the Flaming Dragon travel along its path from the time it reaches its maximum height (labelled t = 0) until it explodes 10 seconds later?
- (d)
- Into what shape and color does the Flaming Dragon explode?