Return to Other Sample Exams.
THIRD HOUR EXAM, MATH 223
Instructor: Kris Green, April 10, 1997
- 1.
- Multiple Choice (5 points each):
- (a)
- The area of the region shown can be computed correctly using which of
the following integrals?
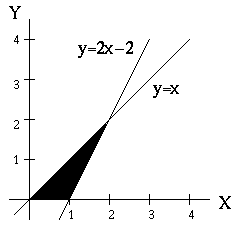
- (b)
- Which of the following vector fields could represent the gradient
field of the function f(x,y) = x2/2 + y?
- (c)
- Which of the following vector fields best matches the verbal
description below? ``The vectors of
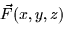 point toward the
origin and have a magnitude which decreases as the point (x,y,z) moves
farther from the origin.''
point toward the
origin and have a magnitude which decreases as the point (x,y,z) moves
farther from the origin.''
- (d)
- The line parameterized by x(t) = 3-2t, y(t) = 1 + t, z(t) = -5 - 3t
is parallel to which vector?
- 2.
- To find the centroid (physical center) of a two dimensional region
R we evaluate the integrals

Find the coordinates (xc, yc) of the region shown here.
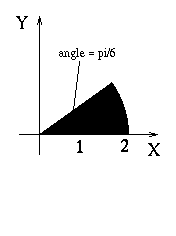
- 3.
- For the integral shown below, first sketch the region of integrations
and then switch the integral to cylindrical or spherical coordinates,
whichever is appropriate. Do not evaluate the integral.
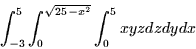
- 4.
- A particle is traveling in a force field along the path
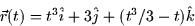
for t > 0.
- (a)
- Is the particle ever traveling purely horizontally (ie. parallel to
the xy plane?) If so, when?
- (b)
- If the particle has a mass of 2 kg and the position is measured in
meters, use the equations
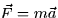 to calculate the force
acting on the particle as a function of time. (Note:
to calculate the force
acting on the particle as a function of time. (Note: 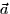 is the
acceleration of the particle.)
is the
acceleration of the particle.)
- (c)
- If the force field is turned off at t = 3 seconds, find the
parametric equations for the resulting motion of the particle.
- (d)
- How far does the particle travel in the first 10 seconds after the
field is turned off?
- 5.
- The path of the earth around the sun can be parameterized (roughly)
by
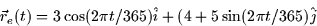
with the sun located at the origin. The comet Hale-Bopp is also orbiting
the sun along the path (completely made up)
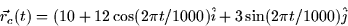
where t is measured in days for both motions.
- (a)
- On the same axes, with the sun located at the origin, draw the paths
of both the earth and the comet. Label the point t= 0 for each, and
indicate the direction of the motion.
- (b)
- Using vector addition (or subtraction) find the parametrization of
the comet's path asseen from the earth. (Be careful...draw the vectors on
your diagram above to see how to do this.)
- (c)
- Using the vector found in the previous part, what algebraic condition
must be satisfied for the comet to hit the earth? Do not try to solve the
equations, but explain your reasoning in one or two sentences.
Vector Calculus
8/20/1998
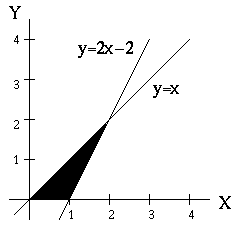
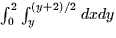
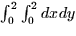
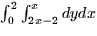
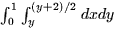
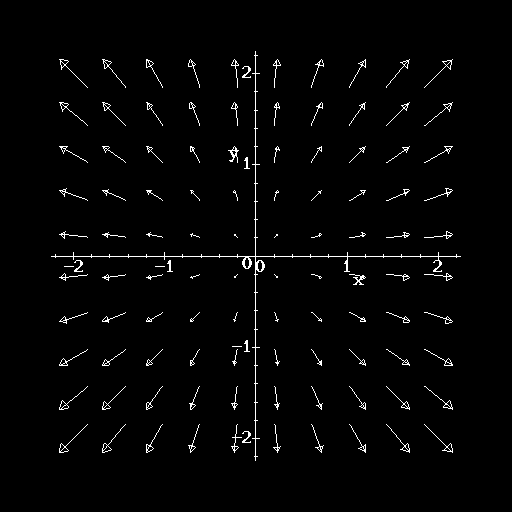
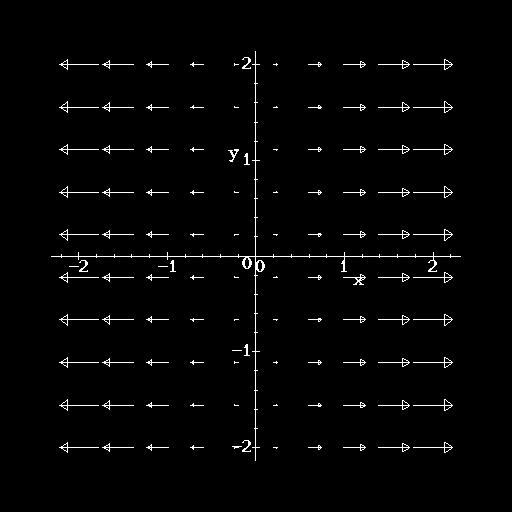

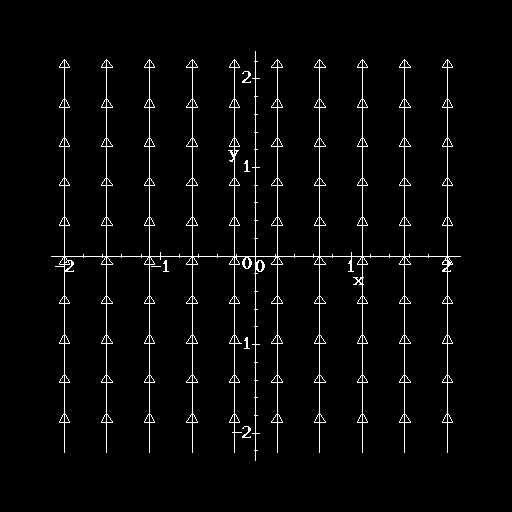
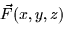 point toward the
origin and have a magnitude which decreases as the point (x,y,z) moves
farther from the origin.''
point toward the
origin and have a magnitude which decreases as the point (x,y,z) moves
farther from the origin.''
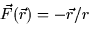
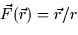
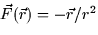
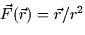
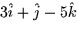
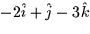
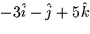
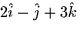
![]()
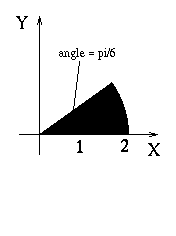
![]()
![]()
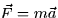 to calculate the force
acting on the particle as a function of time. (Note:
to calculate the force
acting on the particle as a function of time. (Note: 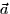 is the
acceleration of the particle.)
is the
acceleration of the particle.)
![]()
![]()