- (a)
- Find the average distance of points in the shaded region to the
y-axis.
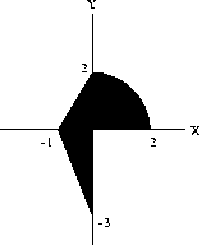
- (b)
- Find the area of the region bounded by the graphs y = x2 and y = 2x - x3.
![]()
- (a)
- Draw the regions of integration.
- (b)
- Rewrite the two iterated integrals as a single integral by reversing the order of integration.
- (c)
- Compute the integral.
![]()
- (a)
- Write down, but do not evaluate, an integral to compute the total mass of the cloud, using Cartesian coordinates.
- (b)
- Choose a better coordinate system and rewrite the integral in this coordinate system.
- (c)
- Mr. Spock claims that the cloud has a mass of 1,642
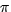 kilograms.
Is he right?
kilograms.
Is he right?
- (d)
- THIS IS A VERY VERY BAD TEST QUESTION.
- (a)
- Set up, and evaluate the flux integral directly.
- (b)
- Use the divergence theorem to compute the flux.
- (a)
- State the divergence theorem. Be sure to use complete sentences, include all necessary conditions, and define all symbols used.
- (b)
- For the vector field
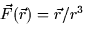 (note:
div
(note:
div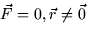 ) a student states the following:
) a student states the following:
``For the surface S being a closed cube of side length 2 centered at the origin with W the enclosed volume, we have
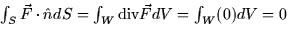 .''
.''
What is wrong with this statement (in complete sentences)?