Return to Other Sample Exams.
THIRD HOUR MAKEUP EXAM
MATH 223
Instructor: Kris Green
April 3, 1998
9:00-9:50
- 1.
- For each of the following, set up, but do not evaluate, a double
integral in an appropriate coordinate system.
- (a)
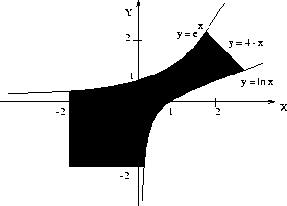
- Find the area of the shaded region below.
- (b)
- Find the average distance to the origin of points in a disk of
radius a that is centered at the origin.
- 2.
- For the integral
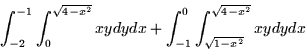
- (a)
- Draw the regions of integration.
- (b)
- Rewrite the integrals as a single integral by changing into polar
coordinates.
- (c)
- Compute the integral.
- 3.
- The Cosmic Egg can be modeled as the region between the lower
hemisphere of a sphere of radius 5 centered at the origin, and the surface
z = 25 - x2 - y2 (all distances are in parsecs.) The density of the
Egg is given by

If the egg has a mass of 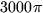 then it
will be capable of hatching a being that will grow large enough to eat the
Milky Way galaxy. Are we in danger of this happening?
then it
will be capable of hatching a being that will grow large enough to eat the
Milky Way galaxy. Are we in danger of this happening?
- 4.
- Calculate the flux of
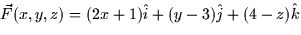 out of the closed cube with
corners at the points (2,0,0), (-1,0,0), (2,0,3), (0,1,0), and (0,-2,0).
out of the closed cube with
corners at the points (2,0,0), (-1,0,0), (2,0,3), (0,1,0), and (0,-2,0).
- 5.
-
- (a)
- State the divergence theorem. Be sure to use complete sentences,
include all necessary conditions, and define all symbols used.
- (b)
- The Blob is attacking Springfield nuclear power plant. It has no
definite shape at any point in time. It swallows a small source of
radioactive fuel that emits radiation along the vector field
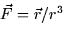 . Calculate the total flux of this vector field out of the
Blob.
. Calculate the total flux of this vector field out of the
Blob.
Vector Calculus
8/20/1998
![]()
![]()
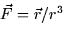 . Calculate the total flux of this vector field out of the
Blob.
. Calculate the total flux of this vector field out of the
Blob.