Return to Other Sample Exams.
Math 223 Name
Fall 1997
Test 3
Directions: Please read each question carefully and show all your work
in doing each question. No partial credit will be given if you do not
show your work. If you have any questions about the test, please ask me.
Your work should of course be your own. Good Luck!
- 1.
- (20 points) Let f(x,y) = x2 + xy.
- (a)
- Find all local minima, local maxima, and saddle points of
f(x,y).
- (b)
- Find the maximum and minimum values, if they exist, of f(x,y)
on xy + x = 1.
- 2.
- (10 points) Let z = f(x,y) be given by the table below.
x  y y |
2 |
2.5 |
3 |
3.5 |
4 |
| 2 |
5.41 |
5.58 |
5.73 |
5.87 |
6 |
| 2.5 |
7.66 |
7.83 |
7.98 |
8.12 |
8.25 |
| 3 |
10.41 |
10.58 |
10.73 |
10.87 |
11 |
| 3.5 |
13.66 |
13.83 |
13.98 |
14.12 |
14.25 |
| 4 |
17.41 |
17.58 |
17.73 |
17.87 |
18 |
Give reasonable upper and a lower bounds for 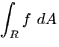 where R is the region given by
where R is the region given by
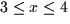 and
and 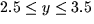 .
.
- 3.
- (15 points) Use a triple integral to find the volume of the region
above the xy-plane
(i.e. 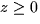 ) bounded by x = 0,
x = 3, and z = 4 - y2.
) bounded by x = 0,
x = 3, and z = 4 - y2.
- 4.
- (15 points) Evaluate
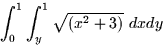 .
. - 5.
- (10 points) Consider the integral
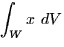 where W is the region above the xy-plane
between the spheres
where W is the region above the xy-plane
between the spheres 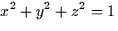 and
and
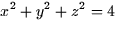 .
Write this integral as a triple integral in spherical coordinates,
but do not evaluate it.
.
Write this integral as a triple integral in spherical coordinates,
but do not evaluate it.
- 6.
- (20 points)
- (a)
- Consider the curve above. Determine which of the choices below is a
parameterization of the curve.
- i.
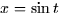 ,
, 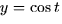 ,
,
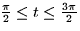 .
.- ii.
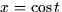 ,
, 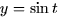 ,
,
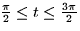 .
.- iii.
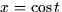 ,
, 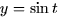 ,
,
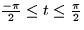 .
.- iv.
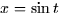 ,
, 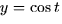 ,
,
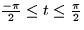 .
.
- (b)
- Suppose the parameterization you chose above describes the motion
of a particle. Find the velocity of the particle at time t = 0.
- 7.
- (10 points) Describe in words the object parameterized by the equations
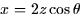 ,
, 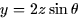 , z = z,
, z = z,
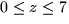 ,
, 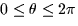 .
.
Vector Calculus
8/21/1998
![]() where R is the region given by
where R is the region given by
![]() and
and ![]() .
.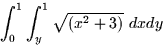 .
.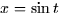 ,
, 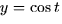 ,
,
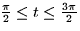 .
.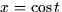 ,
, 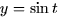 ,
,
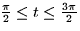 .
.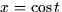 ,
, 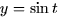 ,
,
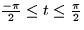 .
.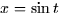 ,
, 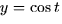 ,
,
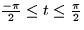 .
.