Return to Other Sample Exams.
THIRD HOUR EXAM, MATH 223
Instructor: Kris Green, December 5, 19967
- 1.
- Multiple Choice (5 points each):
- (a)
- The divergence of the vector field
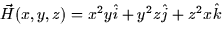 at the point (1,1,-1) is:
at the point (1,1,-1) is:
| a. -2 |
b. 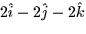 |
c. 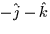 |
d. 2xy + 2yz + 2xz |
- (b)
- The curl of
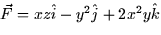 is:
is:
- (c)
- Choose the expression that best describes the vector field shown
below:
(include vector field)
- (d)
- Consider the following line integral:
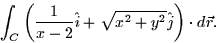
Over which of the following parameterized paths can Green's Theorem be
applied to this integral?
- 2.
- Short answer (10 points each):
- (a)
- Give 3 characterizations of a conservative vector field. If you name
more than 3 correctly, then extra credit will be given. (Hint: One of
these can be the definition of a conservative vector field.)
- (b)
- State Stokes' Theorem and describe the conditions under which it can
be applied.
- 3.
- (10 points) Compute the line integral
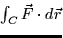 for the vector field
for the vector field
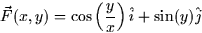
along the path y=x2 from (1,1) to (2,4).
- 4.
- (10 points) Compute the line integral
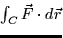 for the vector field
for the vector field
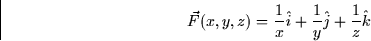
along the path 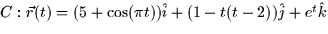 for
for 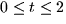 .
. - 5.
- (10 points) Compute the line integral
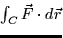 for the vector field
for the vector field
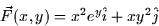
along the square with vertices (2,2), (-2,2), (-2,-2), and (2,-2) in the
counterclockwise direction.
- 6.
- (10 points) Find the flux of
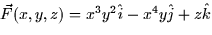 over the portion of
the surface z = 16 - x2 - y2 that lies above the disk
over the portion of
the surface z = 16 - x2 - y2 that lies above the disk  .
. - 7.
- Let
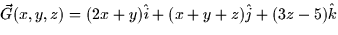 . Compute the flux of
. Compute the flux of  through the sphere of radius 4
centered at (1,-1,0).
through the sphere of radius 4
centered at (1,-1,0).
- 8.
- Find the circulation of
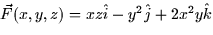 around the triangle in the plane z = y with vertices
(3,0,0), (0,2,2) and (0,0,0) oriented in this order.
around the triangle in the plane z = y with vertices
(3,0,0), (0,2,2) and (0,0,0) oriented in this order.
Vector Calculus
8/20/1998
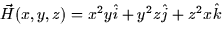 at the point (1,1,-1) is:
at the point (1,1,-1) is:
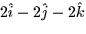
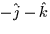
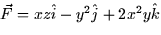 is:
is:
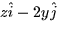
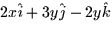

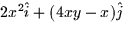
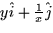
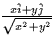
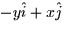
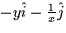
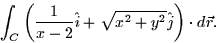
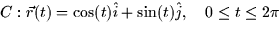
![$C: \vec{r}(t) = [2\cos(t) - 3]\hat{i} + [2\sin(t)-3]\hat{j}, \quad
0 \le t \le 2\pi$](img15.gif)
![$C: \vec{r}(t) = [\cos(t) + 2]\hat{i} + \sin(t)\hat{j}, \quad 0 \le
t \le 2\pi$](img16.gif)
![$C: \vec{r}(t) = [2\cos(t)+5]\hat{i} + [2\sin(t)+5]\hat{j}, \quad 0
\le t \le 2\pi$](img17.gif)
![]()
![]()
![]()