Return to Other Sample Exams.
THIRD HOUR EXAM, MATH 223
Instructor: Kris Green, May 1, 1997
- 1.
- Multiple Choice (5 points each):
- (a)
- The divergence of the vector field
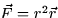 at the
point (1,1,1) is:
at the
point (1,1,1) is:
| a. 5r2 |
b. 1 |
c. 15 |
d.  |
- (b)
- The potential function for the vector field
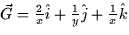 (with x > 0,
y> 0, z > 0) is
(with x > 0,
y> 0, z > 0) is
a. 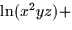 const const |
b.  const const |
| c. Neither of the above |
d. This vector field does not have a potential |
- (c)
- The vector
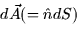 for the upper hemisphere of x2
+ y2 + z2 = 4 oriented toward +z is
for the upper hemisphere of x2
+ y2 + z2 = 4 oriented toward +z is
- (d)
- Suppose you know that a vector field
 has the following
properties: (1) div
has the following
properties: (1) div = 5, and (2) curl
= 5, and (2) curl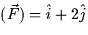 . What is the flux of
. What is the flux of 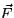 through the cube covering the
region
through the cube covering the
region 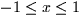 ,
, 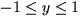 , and
, and 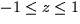 ?
?
- 2.
- Calculate the flux of the vector field
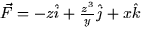 through the upper hemisphere of x2 +
y2 + z2 = 4 that lies above the rectangle
through the upper hemisphere of x2 +
y2 + z2 = 4 that lies above the rectangle 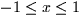 ,
, 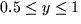 .
. - 3.
- Consider the vector field
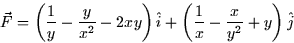
- (a)
- Show that
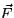 can be written in the form
can be written in the form 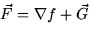 where f(x,y) = (x2 + y2)/xy and
where f(x,y) = (x2 + y2)/xy and 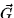 is a non-conservative
vector field.
is a non-conservative
vector field.
- (b)
- Use the previous part to compute the line integral
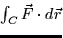 where C is the portion of the parabola y = x2 from x
= 1 to x = 3.
where C is the portion of the parabola y = x2 from x
= 1 to x = 3.
- 4.
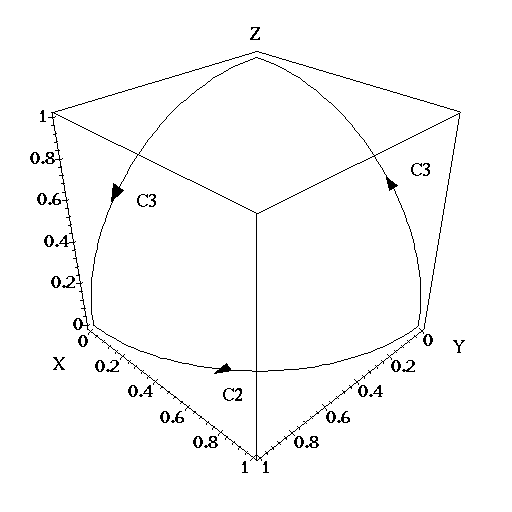
- Consider the circulation of the vector field
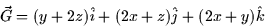
around the boundary of the sphere x2 + y2 + z2 = 1 in the first octant
(ie. x,y,z are all positive.) The figure below illustrates this. Note
that the curve C1 is part of the circle x2 + z2 = 1, C2 is part
of the circle x2 + y2 = 1 and C3 is part of the circle y2 + z2 =
1.
- (a)
- Set up the line integral by parameterizing the path.
- (b)
- Stoke it. (ie. Apply Stokes' theorem.)
- (c)
- Calculate one of these two integrals that you have set up.
- 5.
- Compute the flux of the vector field
 through the triangle in the yz
plane with vertices at (0,0,0), (0,2,4) and (0,0,4) and oriented in the
+x direction.
through the triangle in the yz
plane with vertices at (0,0,0), (0,2,4) and (0,0,4) and oriented in the
+x direction.
Vector Calculus
8/20/1998
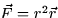 at the
point (1,1,1) is:
at the
point (1,1,1) is:

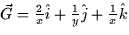 (with x > 0,
y> 0, z > 0) is
(with x > 0,
y> 0, z > 0) is
 const
const const
const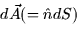 for the upper hemisphere of x2
+ y2 + z2 = 4 oriented toward +z is
for the upper hemisphere of x2
+ y2 + z2 = 4 oriented toward +z is
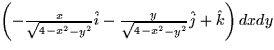
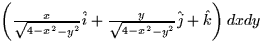
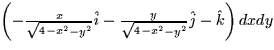
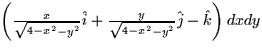
 has the following
properties: (1) div
has the following
properties: (1) div = 5, and (2) curl
= 5, and (2) curl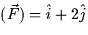 . What is the flux of
. What is the flux of  through the cube covering the
region
through the cube covering the
region  ,
, 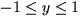 , and
, and 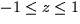 ?
?
![]()
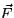 can be written in the form
can be written in the form 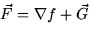 where f(x,y) = (x2 + y2)/xy and
where f(x,y) = (x2 + y2)/xy and 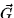 is a non-conservative
vector field.
is a non-conservative
vector field.
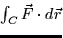 where C is the portion of the parabola y = x2 from x
= 1 to x = 3.
where C is the portion of the parabola y = x2 from x
= 1 to x = 3.
![]()
