Return to Other Sample Exams.
FOURTH HOUR EXAM
MATH 223
Instructor: Kris Green
May 1, 1998
9:00-9:50
- 1.
- Consider the motion of a particle described by the parametric curve
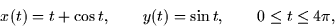
- (a)
- Is the motion periodic? (ie. does it ever repeat its movements?)
- (b)
- Does the motion ever come to a complete stop? If so, when?
- (c)
- Is the motion ever purely horizontal (x-direction)? If so,
when?
- (d)
- Is the motion ever purely vertical (y-direction)? If so, when?
- (e)
- Using what you know about the motion of a particle along the path
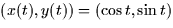 for
for  , describe in
complete sentences the motion of the particle above.
, describe in
complete sentences the motion of the particle above.
- 2.
- For the vector field
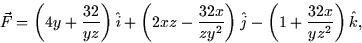
- (a)
- Show that
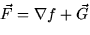 where
where

and 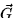 is a non-conservative vector field.
is a non-conservative vector field.
- (b)
- Use part (a) (the fact that
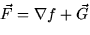 , and you
know what f and
, and you
know what f and 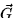 are) to compute
the work done by the force
are) to compute
the work done by the force 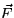 along the path C from (1,1,1) to
(2,8,4) along the curve (t,t3,t2).
along the path C from (1,1,1) to
(2,8,4) along the curve (t,t3,t2).
- 3.
- Given the vector field
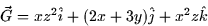
and the closed path, C, formed by the semicircles  (in the xy-plane) and
(in the xy-plane) and 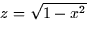 (in the xz-plane) and
oriented counter-clockwise when viewed from the +z axis,
calculate the circulation of
(in the xz-plane) and
oriented counter-clockwise when viewed from the +z axis,
calculate the circulation of 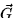 around C, using Stokes'
Theorem. Note that there is an obvious surface, S, which has the curve
C as its boundary. Graphing these curves on the same set of xyz-axes
this may help.
around C, using Stokes'
Theorem. Note that there is an obvious surface, S, which has the curve
C as its boundary. Graphing these curves on the same set of xyz-axes
this may help.
- 4.
- For each of the following situations, explain (using complete
sentences, possibly supported by calculations and/or diagrams) why Green's
Theorem can not be directly applied. If a modification to Green's
Theorem (such as the addition of a negative) will correct the problem,
explain this.
- (a)
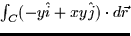 , C is the path
, C is the path
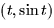 for
for 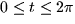 .
. - (b)
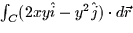 , where
, where
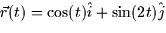 for
for 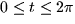 .
. - (c)
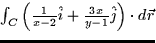 where C is the circle of radius 4 centered at
(1,1) traversed counter-clockwise.
where C is the circle of radius 4 centered at
(1,1) traversed counter-clockwise.
- 5.
- For the illustrated paths and vector fields below, decide whether the
line integral
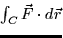 is positive, negative, or
zero.
is positive, negative, or
zero.
- (a)

- (b)
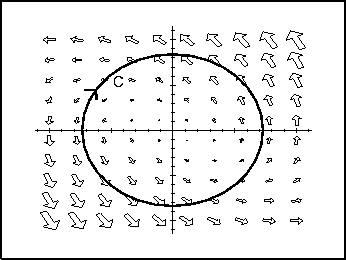
- (c)
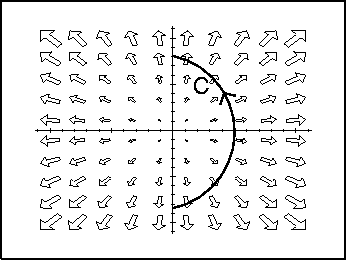
- (d)
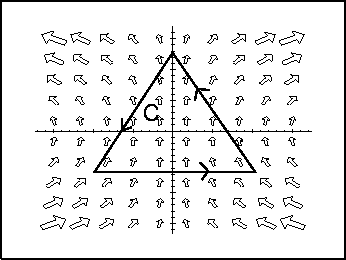
Vector Calculus
8/20/1998
![]()
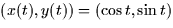 for
for 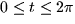 , describe in
complete sentences the motion of the particle above.
, describe in
complete sentences the motion of the particle above.
![]()
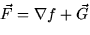 where
where

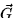 is a non-conservative vector field.
is a non-conservative vector field.
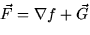 , and you
know what f and
, and you
know what f and 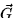 are) to compute
the work done by the force
are) to compute
the work done by the force 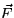 along the path C from (1,1,1) to
(2,8,4) along the curve (t,t3,t2).
along the path C from (1,1,1) to
(2,8,4) along the curve (t,t3,t2).
![]()
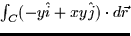 , C is the path
, C is the path
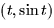 for
for 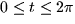 .
. 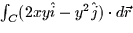 , where
, where
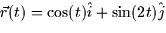 for
for 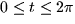 .
. 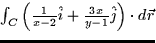 where C is the circle of radius 4 centered at
(1,1) traversed counter-clockwise.
where C is the circle of radius 4 centered at
(1,1) traversed counter-clockwise.



