Return to Other Sample Exams.
Math 223 Name
Fall 1997
Test 4
Directions: Please read each question carefully and show all your work
in doing each question. No partial credit will be given if you do not
show your work. If you have any questions about the test, please ask me.
Your work should of course be your own. Good Luck!
- 1.
- (10 points) On the gradient field below sketch and label 4 possible
contours of an associated potential function.
- 2.
- (15 points) Suppose the wind exerts a force on a sailboat
given by the vector field
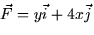 .Find the amount of work done by the wind to move the sailboat
along the path y = x2 from (0,0) to (1,1).
.Find the amount of work done by the wind to move the sailboat
along the path y = x2 from (0,0) to (1,1).
- 3.
- (15 points) Consider the function
f(x,y,z) = x3 - 4x2 y + y4. Find
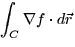 where C is
part of a helix given by
where C is
part of a helix given by 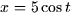 ,
, 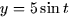 ,and
,and 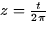 for
for 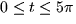 .
. - 4.
- (20 points) Consider the vector field
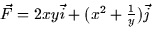 .
.
- (a)
- Compute
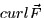 . Can you determine from your computation
whether or not
. Can you determine from your computation
whether or not 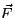 has a potential function? Explain your
conclusion.
has a potential function? Explain your
conclusion.
- (b)
- Try to construct a potential function for
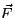 . Is
the result of your attempt consistent with your answer above? Why
or why not?
. Is
the result of your attempt consistent with your answer above? Why
or why not?
- 5.
- (15 points) Given
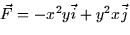 ,find
,find 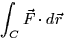 where C is
a circle of radius 2 centered at the origin with counterclockwise
orientation.
where C is
a circle of radius 2 centered at the origin with counterclockwise
orientation.
- 6.
- (10 points) Without actually computing the flux, determine whether
the flux of
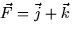 through the surmface
z = 4 for
through the surmface
z = 4 for 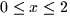 and
and 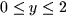 with
upward orientation is positive, negative, or zero. Explain your
reasoning.
with
upward orientation is positive, negative, or zero. Explain your
reasoning.
- 7.
- (15 points) Evaluate
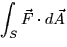 where
where
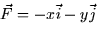 and S is the surface
given by
and S is the surface
given by
f(x,y) = x2 + y2 for 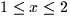 and
and
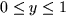 with upward orientation.
with upward orientation.
Vector Calculus
8/21/1998
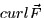 . Can you determine from your computation
whether or not
. Can you determine from your computation
whether or not 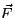 has a potential function? Explain your
conclusion.
has a potential function? Explain your
conclusion.
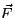 . Is
the result of your attempt consistent with your answer above? Why
or why not?
. Is
the result of your attempt consistent with your answer above? Why
or why not?