-
Composition of Functions
- This is one way of making a new function from two old
functions. Essentially, we take one function and ”plug it into” the other function. For
example, if we compose f(x) = 2x3 and g(x) = 4x-5 we get either h(x) = (f ∘g)(x) =
f(g(x)) = 2(4x - 5)3 or we get k(x) = (g ∘ f)(x) = 4(2x3) - 5 depending on the order
of the composition. In general, the two orders are not the same.
-
Chain rule
- We’ll be using this rule a lot. The symbolic analysis section will explain it in
more detail, but the basic idea is that if you have a function composed with another
function and you need the derivative of the combined object, you use the chain rule
to ”chain together” derivatives of each function. For example, if we start with the
functions f(x) and g(x) above and compose them into h(x) the new function h is no
longer a simple power function or polynomial (although we could multiply it out into
a polynomial.) But since it is composed of these simpler functions, we can still take
it’s derivative. In fact, the chain rule says that
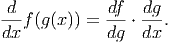
Thus h′(x) = [df∕dg][dg∕dx] = [2 ⋅ 3g(x)2] ⋅ [4] = 24(4x - 5)2. A derivation and proof of the
chain rule are somewhat technical; for now, think of this as a way of chaining together the
derivatives so the objects which look like (but aren’t really) fractions will cancel out. In the
above illustration of the chain rule, the first ”fraction” has the numerator we
want (df) and the second ”fraction” has the denominator we want (dx). Each of
these ”fractions” has a dg term that ”cancels out” to give the derivative we want:
df∕dx.
-
Product rule
- The product rule allows us to take derivatives of functions that are products of
simpler functions. It says that
![-d- -df- dg-
dx [f(x) ⋅ g(x)] = g (x ) ⋅dx + f(x) ⋅dx .](Text_Fall_2014290x.png)
The proof of this rule will be given in the symbolic analysis section, and will make use of the
derivative of a logarithm and the chain rule.
-
Quotient rule
- The product rule allows us to take derivatives of functions that are products of
simpler functions. It says that
![[ ] ′ ′
-d- f-(x) = g-(x-)f(x-) --f-(x-)g(x)
dx g(x) [g(x )]2](Text_Fall_2014291x.png)
The proof of this rule will be given in the symbolic analysis section, and will make use of the
derivative of a logarithm and the chain rule.
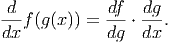
![-d- -df- dg-
dx [f(x) ⋅ g(x)] = g (x ) ⋅dx + f(x) ⋅dx .](Text_Fall_2014290x.png)
![[ ] ′ ′
-d- f-(x) = g-(x-)f(x-) --f-(x-)g(x)
dx g(x) [g(x )]2](Text_Fall_2014291x.png)