Ellipses

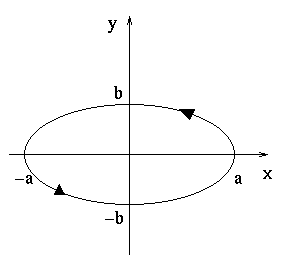
An ellipse is very similar to a circle. In fact, if you recall the equation for the ellipse shown below

you will note that it can be written in the form

$$\left( \frac{x}{a} \right)^2 + \left( \frac{y}{b} \right)^2 = 1.$$ (20)

This is very similar to the circle equation and defining x and y as functions of t in the obvious fashion we obtain

$$\vec{r}(t) = a \cos t \hat{i} + b \sin t \hat{j}.$$ (21)

The main difference from the circle is that the amplitudes of the sine and cosine terms are different.

Example. Find the parameterization of the ellipse centered at (1,3,5) passing through the points (4,3,5) and (1,5,5) oriented counterclockwise as seen from the +z axis.

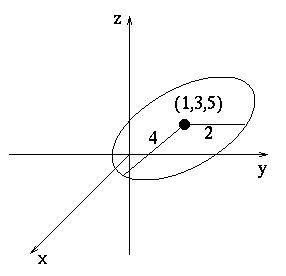
From the picture, we can see that the center is $\vec{r}_0 = \hat{i} + 3 \hat{j} + 5 \hat{k}$. As seen from the center, the ellipse should have the equation $\vec{s}(t) = 3 \cos t \hat{i} + 2 \sin t \hat{j}$. Using vector addition, we get the parameterization from the origin as

$$\vec{r}(t) = (1 + 3 \cos t) \hat{i} + (3 + 2 \sin t) \hat{j} + 5 \hat{k}.$$ (22)