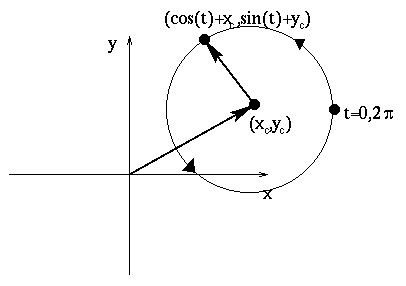We know (hopefully) that the equation x2 + y2 = a2 represents a circle of radius a centered at the origin. We can rewrite this equation as
| (18) |
Noting that if we let
| (19) |
then the parameterization ![]() will trace out the circle. This particular
parameterization
starts at the point (a,0) and traces the curve counterclockwise as t
increases. How could we start the circle at the point (0,1)? There are
two obvious ways (and other not-as-obvious ways):
will trace out the circle. This particular
parameterization
starts at the point (a,0) and traces the curve counterclockwise as t
increases. How could we start the circle at the point (0,1)? There are
two obvious ways (and other not-as-obvious ways):
Of these choices, the second is probably better in the sense that the range of t starts at 0.
How can we trace the circle put clockwise instead of counter clockwise?
One way is to let t become -t. Then the parameterization (using some
properties of sine and cosine) becomes ![]() .
.
How can we center the circle at a point ![]() ? To do this, use the picture below to help with the
vector addition. The result is
? To do this, use the picture below to help with the
vector addition. The result is ![]() .
.