Lines

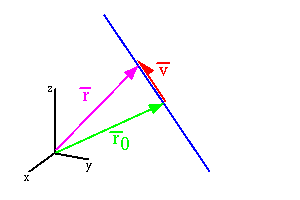
Parameterizing a striaght line requires two pieces of information:

1.

We need at least one point on the line. we'll call this point (x₀,y₀,z₀) and label it as a vector $\vec{r}_0 = x_0 \hat{i} + y_0 \hat{j} + z_0 \hat{k}$.

2.

We need the direction in which the line points. This is a vector, and we'll refer to it as $\vec{v}$.

In order to parameterize the line, we use vector addition. A scalar multiple of $\vec{v}$ still points in the same direction as $\vec{v}$. Let the first point on the line be $\vec{r}_0$. Another point on the line can be obtained by adding $\vec{v}$ to $\vec{r}_0$ as shown in the figure below. If we continue to add scalar multiples of $\vec{v}$ to the initial point, we can get the whole line. By letting t be a parameter which multiplies $\vec{v}$ we get the parameterization of the line via vector addition as

$$\vec{r}(t) = \vec{r}_0 + t \vec{v}.$$ (15)

Example. What is the parameterization of the line segment which starts at (1,0,5) and ends at (-4, 2, 0)?

If we let $\vec{r}_0 = \hat{i} + 5 \hat{k}$ and $\vec{r}_1 = -4 \hat{i} + 2\hat{j}$, then a displacement vector that is parallel to the line would be

$$\vec{v} = \vec{r}_1 - \vec{r}_0 = -5 \hat{i} + 2 \hat{j} -5\hat{k}.$$ (16)

So, as t ranges from 0 to 1, the parameterization

$$\vec{r}(t) = \vec{r}_0 + t \vec{v} = (1 - 5t)\hat{i} + 2t \hat{j} + (5 - 5t) \hat{k}$$ (17)

traces out the line segment.