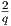 represents the average cost for producing q of a product.
(Assuming that q > 0.) Find the minimum average cost and the number of goods that should be
produced in order to achieve this minimum.
represents the average cost for producing q of a product.
(Assuming that q > 0.) Find the minimum average cost and the number of goods that should be
produced in order to achieve this minimum.
14.1. The function (q) = 0.1q + 3 + 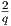 represents the average cost for producing q of a product.
(Assuming that q > 0.) Find the minimum average cost and the number of goods that should be
produced in order to achieve this minimum.
represents the average cost for producing q of a product.
(Assuming that q > 0.) Find the minimum average cost and the number of goods that should be
produced in order to achieve this minimum.
14.2. The function (q) = 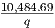 - 2.250 + 0.000328q gives the average cost for producing q
goods.
- 2.250 + 0.000328q gives the average cost for producing q
goods.
14.3. Given the points (1, 12), (2, 7), (3, 5) and (4, 6), assume that a linear function fits these points. Assume that the linear function passes through the point (,) so that the y-intercept, A, is given by A = - B where B is the slope of the least-squares regression line.