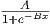[next] [prev] [prev-tail] [tail] [up]

Mechanics and Techniques Problems

15.1. For each of the following functions, compute the first derivative of the function with respect to the independent variable.

  1. f(x) = 3 ln(x) + 5
  2. h(t) = -2e3t
  3. g(s) = 5s + 3s ln(s2 - 4)
  4. p(y) = 5ye-y2
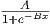  5. The logistic function f(x) = ---A-Bx 1+e, where A and B are constants.

15.2. Find the local maxima and minima of the function given in 1d) above. Use this information to help sketch a picture of what the function looks like when plotted as p(y) versus y.

15.3. The present value of an investment is the amount of money you would need to invest at a particular interest rate r for a specified period of time t in order for the investment to rise to a total value of V .

  1. Assuming that there are n compounding periods per year, determine a formula for the present value of an investment.
  2. Assuming that the interest is compounded continuously, determine a formula for the present value of an investment.
  3. Using your formulas in a) and b) fill in the table showing the present value of a 10-year investment that has a value of $1 million. Your table should compute this for the following range of interest rates: 1%, 2.5%, 5% and should show the results for annual compounding, monthly compounding, daily compounding and continuous compounding.

    Interest Rate

    Annual compounding

    Monthly compounding

    Daily compounding

    Continuous compounding

    1%

    2.5%

    5%

[next] [prev] [prev-tail] [front] [up]