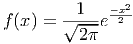
17.1. A standard normal distribution is a normal distribution whose mean is 0 and whose standard deviation is 1. The function that gives rise to the standard normal distribution is:
17.2. A few years ago, you set up an internet business that initially brought in $30,000 revenue and $800 per year thereafter. At start up time, you immediately invested this income stream at 6% interest compounded continuously. You want $1,000,000 to accrue from this investment in order to retire. After how many years will you be able to retire? Hint: Set x0 = 0 in the Basic Integration Tool, replace the function in C9 with the appropriate function for this problem, and change xN (which is T in the integral you need) until you hit your goal.
17.3. The management of Fitter Than Thou Health Spa is considering renovating its exercise room and buying new equipment. It has developed two plans. Plan 1 costs $700,000 to renovate the room, buy the equipment and then install it. It is expected to generate an income stream of $550,000 per year over the next 5 years. Plan 2 requires less initial outlay at $250,000 but will generate an income stream of only $470,000 per year for the next 5 years. If the interest rate is expected to hold at 8% per year for the next 5 years,
17.4. The demand function for a collapsible pull-along sports carrier is
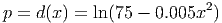
where p is the unit price in hundreds of dollars and x is the quantity demanded per week. The corresponding supply function is
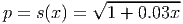
where p is the unit price and x is the number of carriers the supplier is willing to make available at price p.