10.1 Which coefficients are trustworthy?

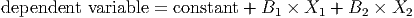
In the last chapter, several regression models of EnPact’s employee salary structure were developed in order to determine if female employees earn less than their male counterparts. These models indicate that females do earn less than their male counterparts, often many thousands of dollars a year less, depending on which variables are used in the models. As EnPact’s Human Resources Director, you are aware that if females do indeed earn substantially less than males, say $5000 a year, then EnPact could be liable for a potentially ruinous multi-million dollar law suit. But to what degree can you be confident that these models are indeed producing accurate results?

We will answer this question and related questions in this chapter, but first we need some concepts.

Suppose we have a regression equation with two explanatory variables, X₁ and X₂, and their coefficients, and , respectively:

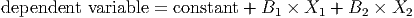
If one of the coefficients is zero, say B₁, then X₁ makes no contribution to the dependent variable no matter what value it takes on because 0 × X₁ = 0 and the equation reduces to

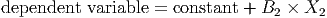
In this case, X₁ is said to be insignificant.

Just because a coefficient is nonzero, however, does not mean that the variable is necessarily significant. A statistician would warn us that regression coefficients are only estimates² and that some of them, in fact, should–or rather could–be zero. The question is, then, can we identify which variables could possibly have zero coefficients and thus be eliminated from our analysis because they are insignificant? The answer is: not with 100% certainty–but we can be 95% confident as to which variables are significant and which are not. When statisticians use the phrase, ”95% confident,” they mean that 95% of the time we will be able to correctly identify whether a particular variable is or is not significant.

We need to understand two formulations concerning what it means to say that a variable is significant:

1. A variable is significant if we are 95% confident that its coefficient is nonzero is equivalent to saying
2. A variable is significant if there is less than a 5% chance that its coefficient is zero.

Both of these perspectives concerning the significance of a variable are given to us in regression output and provide slightly different information.