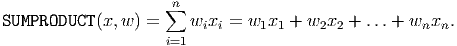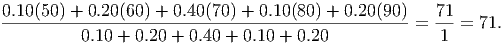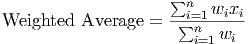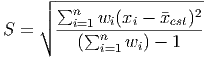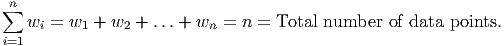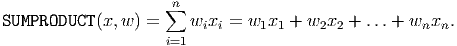Another way to think of weighted averages is to think of lining up the data in one
column and the weights in another column. By multiplying line-by-line, we find the
contribution of each item to the weighted average. Adding these contributions results in
calculating the top part of a weighted average. In Excel, the SUMPRODUCT function takes
two lists (one is data, one is weights) and carries out this computation. This is equivalent to
thinking of the items as a vector and the weights as a vector and computing the vector dot
product or scalar product.
If the two lists are given by x = (x1,x2,…,xn) and w = (w1,w2,…,wn), the scalar product or
SUMPRODUCT of these two lists is simply