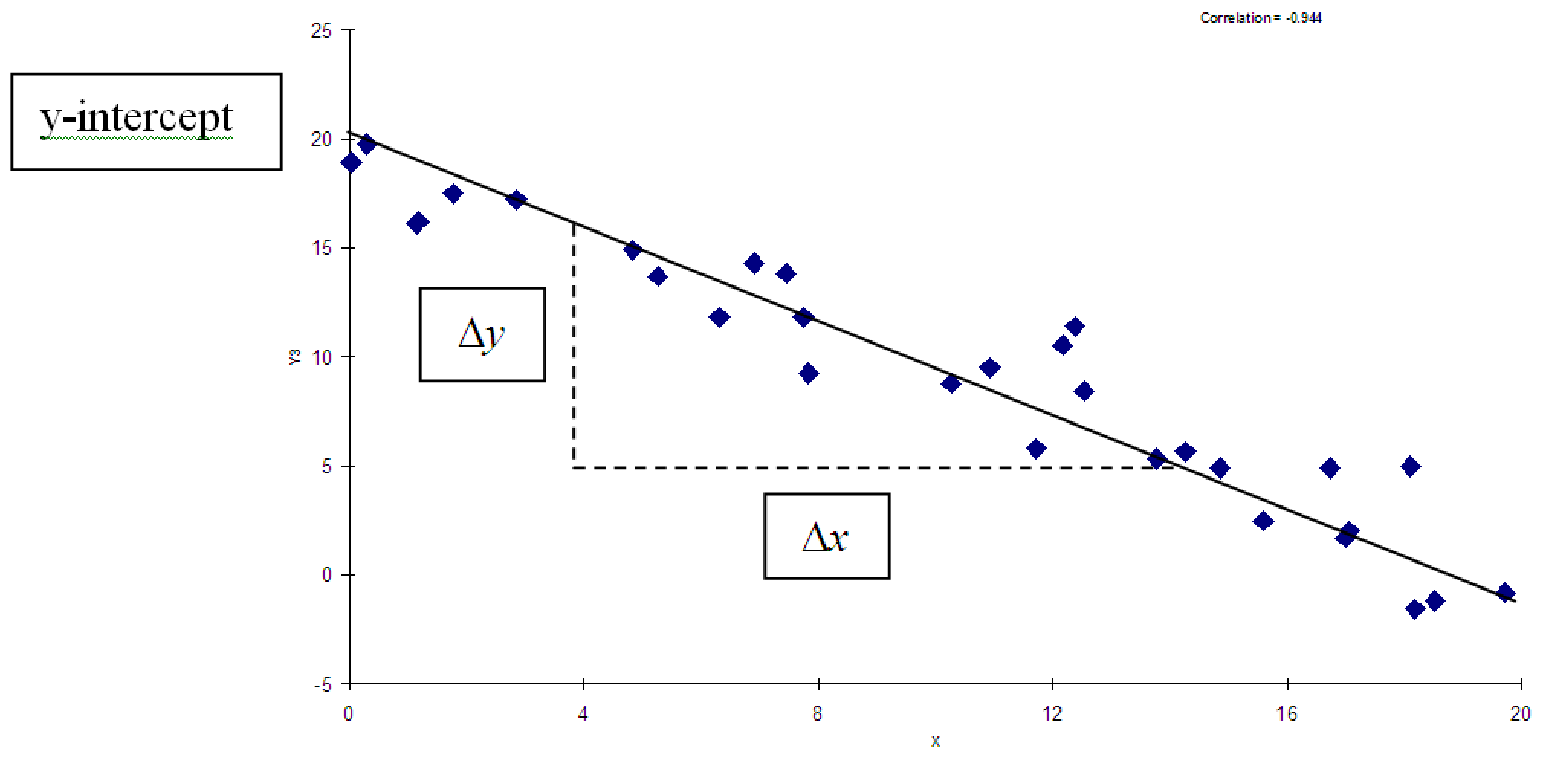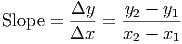
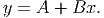
In this equation, A is the y-intercept and B is the slope. The two other letters represent the variables: x is the independent variable, y is the dependent variable.
The equation can also be represented in point-slope form:
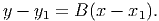
where B is again the slope and (x1,y1) is a point on the line. Both forms are equivalent; they are simply written in a different form to make it easier to use one or the other, depending on which two pieces of information you have. For example, if you re-arrange the point-slope form, you can produce y = Bx + (y1 - Bx1), showing that the y-intercept A = y1 - Bx1.