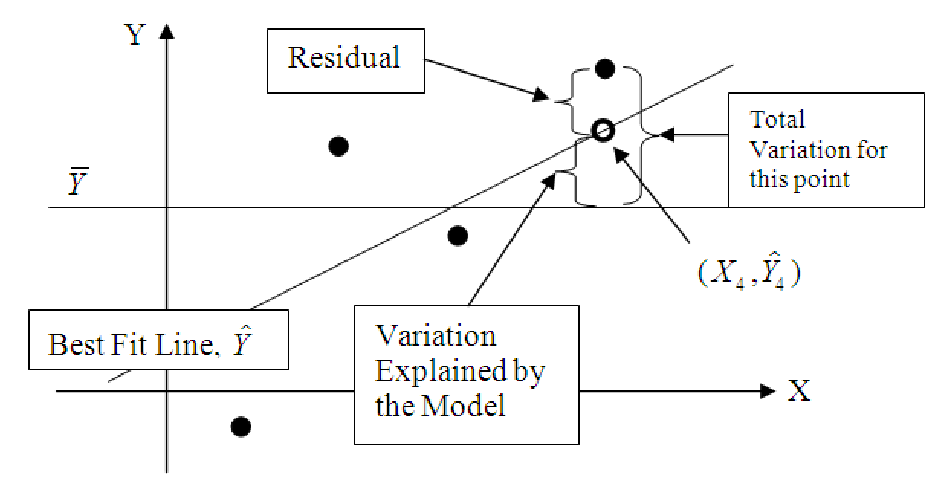
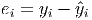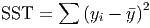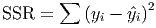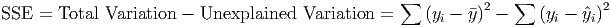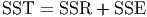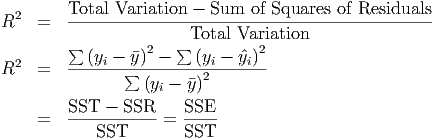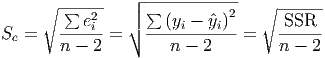-
Predicted values (fitted values)
- These are the predictions of the y-data from using the
model equation and the values of the explanatory variables. They are denoted by the
symbol ŷi.
-
Observed values
- These are the actual y-values from the data. They are denoted by the
symbol yi.
-
Residuals
- This is the part that is left over after you use the explanatory variables to predict
the y-variable. Each observation has a residual that is not explained by the model
equation. Residuals are denoted by ei and are computed by
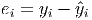
Since these are computed from the y values, it should be clear that the residuals have the
same units as the y, or response, variable.
-
Total Variation (Total Sum of Squares, SST)
- The total variation in a variable is the sum
of the squares of the deviations from the mean. Thus, the total variation in y
is
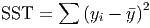
-
Unexplained variation (Sum of Squares of Residuals, SSR)
- The variation in y that is
unexplained is the sum of the squares of the residuals:
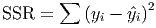
-
Explained variation (Sum of Squares Explained, SSE)
- The total variation in y is
composed of two parts: the part that can be explained by the model, and the part that
cannot be explained by the model. The amount of variation that is explained
is
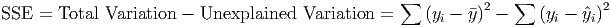
-
Regression Identity
- One will note that the Total Variation is equal to the sum of the
Unexplained Variation and the Explained Variation.
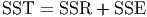
-
Coefficient of Determination (R2)
- This is a measure of the ”goodness of fit” for a regression
equation. It is also referred to as R-squared (R2) and for simple regression models it is the
square of the correlation between the x- and y-variables. R2 is really the percentage of the
total variation in the y-variable that is explained by the x-variable. You can compute R2
yourself with the formula
R2 is always a number between 0 and 1. The closer to 1 the number is, the more confident
you can be that the data really does follow a linear pattern. For data that falls
exactly on a straight line, the residuals are all zero, so you are left with R2 =
1.
-
Degrees of Freedom for a linear model
- The degrees of freedom for any calculation are the
number of data points left over after you account for the fact that you are estimating certain
quantities of the population based on the sample data. You start with one degree of
freedom for each observation. Then you loose one for each population parameter
you estimate. Thus, in the sample standard deviation, one degree of freedom is
lost for estimating the mean. This leaves you with n - 1. For a linear model, we
estimate the slope and y-intercept, so we loose two degrees of freedom, leaving
n - 2.
-
Standard Error of Estimate (Se)
- This is a measure of the accuracy of the model for making
predictions. Essentially, it is the standard deviation of the residuals, except that there are
two population parameters estimated in the model (the slope and y-intercept of the
regression equation), so the number of degrees of freedom is n - 2, rather than the normal
n - 1 for standard deviation.
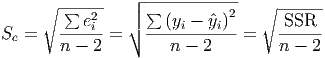
The standard error of estimate can be interpreted as a standard deviation. This means that
roughly 68% of the predictions will fall within one Se of the actual data, 95% within two, and
99.7% within three. And since the standard error is basically the standard deviation of the
residuals, it has the same units as the residuals, whcih are the same as the units of the
response variable, y.
-
Fitted values vs. Actual values
- This is one of the most useful of the diagnostic graphs that
most statistical packages produce when you perform regression. This graph plots the points
(yi,ŷi) . If the model is perfect (R2 = 1) then you will have y
1 = ŷ1, y2 = ŷ2, and so on, so
that the graph will be a set of points on a perfectly straight line with a slope of 1
and a y-intercept of 0. The further the points on the fitted vs. actual graph are
from a slope of 1, the worse the model is and the lower the value of R2 for the
model.
-
Residuals vs. Fitted values
- This graph is also useful in determining the quality of the
model. It is a scatterplot of the points (ŷi,ei) = (ŷi,ŷi - yi) and shows the errors
(the residuals) in the model graphed against the predicted values. For a good
model, this graph should show a random scattering of points that is normally
distributed around zero. If you draw horizontal lines indicating one standard error
from zero, two standard errors from zero and so forth, you should be able to get
roughly 68% of the points in the first group, 95% in the first two groups, and so
forth.