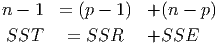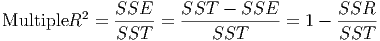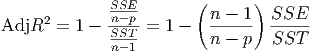-
Multiple linear function
- This is a model much like a normal linear model, except that it
includes several explanatory variables. If the explanatory variables are labeled X1, X2,
… and the response variable is Y , then a multiple-linear model for predicting Y would
take the form
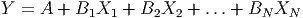
Notice that the multiple linear function has a ”y-intercept” given by A. Each
of the coefficients (the Bi’s) is a slope associated with one of the explanatory
variables.
An important difference between linear and multiple linear models is the graphical
illustration of each. A linear function describes a line in two dimensions. A multiple linear
function with two explanatory variables describes a plane in three-dimensional space. If there
are more than two explanatory variables, we cannot picture the ”hyperplane” that the
function describes.
-
Multiple linear regression
- The process by which you can ”least squares fit” a multiple linear
function to a set of data with several explanatory variables.
-
Stepwise regression
- This is an automated process for determining the best model for a response
variable, based on a given set of possible explanatory variables. The procedure involves
systematically adding the explanatory variables, one at a time, in the order of most influence.
For each variable, a p-value is determined. The user controls a cut-off for the
p-values so that any variable with a p-value above the cut-off gets left out of the
model.
-
p-values
- A p-value is a probability assigned to determine whether a given hypothesis is true or
not. In regression analysis, p-values are used to determine whether or not a given explanatory
variable should have a coefficient of ”0” in the regression model. If the p-value is above 0.05
(5%) then one can usually leave the variable out and get a model that is almost as
good.
| p < 0.05 | Keep the variable |
| p > 0.05 | Drop the variable |
-
Controlling variables
- This is the process by which the person modeling the data tries to
account for data which may have several observations that are similar in some variables, but
differ in others. For example, in predicting salaries based on education, you should control for
experience, otherwise the model will not be very accurate, since several employees
may have the same education, but different salaries because they have different
experience.
-
Degrees of Freedom for Multiple Regression Models
- In multiple regression models, one is
usually estimating several characteristics of the population that underlies the data. For each
of these estimated characteristics, one degree of freedom is lost. If there are n
observations, and you are estimating a multiple regression model with p explanatory
variables, then you loose p + 1 degrees of freedom. (The ”+1” is for the y-intercept.)
Thus,
Also notice that in the ANOVA table for multiple regression, the degrees of freedom of
the Explained (p - 1) plus the degrees of freedom of the Unexplained (n - p)
add up to the degrees of freedom of the sum of the squares of the total variation
(n - 1):
(Total Variation = Sum of Squares of Unexplained + Sum of Squares of Explained)
-
Multiple R2
- This is the coefficient of multiple determination used to determine the quality of
multiple regression models.
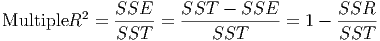
| SSR= | Sum of the squares of the residuals (unexplained variation) |
| SSE = | Explained amount of variation |
| SST = | Total variation in y |
Multiple R2 is the coefficient of simple determination R-Squared between the responses y
i
and the fitted values ŷi.
A large R2 does not necessarily imply that the fitted model is a useful one. There
may not be a sufficient enough number of observations for each of the response
variables for the model to be useful for values outside or even within the ranges of the
explanatory variables, even though the model fits the limited number of existing
observations quite well. Moreover, even though R2 may be large, the Standard
Error of Estimate (Se) might be too large for when a high degree of precision is
required.
-
Multiple R
- This is the square root of Multiple R2. It appears in multiple regression output under
”Summary Measures”.
-
Adjusted R2
- Adding more explanatory variables can only increase R2, and can never reduce it,
because SSE can never become larger when more explanatory variables are present in the
model, while SSTO never changes as variables are added (see the definition of multiple R2
above). Since R2 can often increase by throwing in explanatory variables that may artificially
inflate the explained variation, the following modification of R2, the adjusted R2, is one way
to account for the addition of explanatory variables: This adjusted coefficient of multiple
determination adjusts R2 by dividing each sum of squares by its associated degrees of
freedom (which become smaller with the addition of each new explanatory variable to the
model):
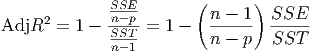
The Adjusted R2 becomes smaller when the decrease in SSE is offset by the loss of a degree
of freedom in the denominator n - p.
-
Full Regression Model
- The full regression model is the multiple regression model that is made
using all of the variables that are available.
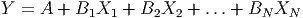
![Df = n - (p + 1 )
= n - p - 1 [Removing parentheses]](Text_Fall_2014131x.png)