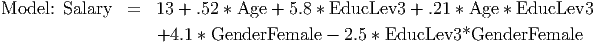
Example 10.5. Creating and interpreting interaction terms from the EnPact
data
An interaction term can be created from a numerical variable and a categorical variable:
| Variable Type | Variable Name | Categories |
| The numerical variable | Age | N/A |
| The categorical variable | EducLev | EducLev1, EducLev2, EducLev3, EducLev4, EducLev5 |
| The interaction variable | Age*EducLev | Age* EducLev1, Age* EducLev2, Age* EducLev3 Age* EducLev4, Age* EducLev5 |
We will interpret a rather simple model built on Age, EducLev3 and Age × EducLev3 where EducLev1 indicates a high-school grad and has been chosen as the reference category for the categorical variable EducLev, and EducLev3 indicates a college grad.
Model: Salary = 12 + .56*Age + 5.2*EducLev3 + .22*Age* EducLev3
Interpretation: When EducLev3 has the value 1, a college graduate is indicated. After substituting 1 for EducLev3 in the model equation, we have
Salary =12 + .56*Age + 5.2*1 + .22*Age* 1
After combing the Age terms, we have a college grad’s salary:
Salary = 17.2 + .78*Age (1)
When EducLev3 has the value 0, a high-school graduate is indicated. After substituting 0 for EducLev3 in the model equation, we have
Salary =12 + .56*Age + 5.2*0 + .22*Age* 0
Simplifying, we have a high-school grad’s salary:
Salary =12 + .56*Age (2)
Comparing equations (1) and (2), we see that a college grad receives a bonus of $5200 (17.2-12=5.2) for having a college degree plus an additional $220 (.78-.56=.220) for each year that he or she has lived compared to a high-school grad of the same age. At age 30, for example, a high-school grad earns $28,800 whereas a 30-year old college grad earns $40,600. At age 60, they earn $45,600 and $64,000, respectively.
Example 10.6. An interaction terms created from two categorical variables
Suppose we have the variables Gender and EducLev from the previous example, and we plan to construct an interaction term using these variables.
| Gender: | GenderFemale, GenderMale |
| Reference category: GenderMale | |
| EducLev: | EducLev1, EducLev2, EducLev3, EducLev4, EducLev5 |
| Reference category: EducLev1 | |
There are 2x5, or 10, interaction terms involved in the interaction variable Gender*Ed. Not all 10 can be submitted to a regression routine, however. Only those interaction terms that do not contain a reference for either variable may be submitted to the regression routine. The following interaction terms are the only ones that may be submitted to a regression routine:
EducLev2*GenderFemale
EducLev3*GenderFemale
EducLev4*GenderFemale
EducLev5*GenderFemale
The other interaction terms cannot be submitted to because each contains either one or both of the reference categories (in bold) from which they are created: EdLev1* GenderMale, EducLev1*GenderFemale , EducLev2*GenderMale, EducLev3 * GenderMale, EducLev4 * GenderMale, EducLev5* GenderMale. This means that each of these is a reference category for the interaction variable EducLev*Gender.
We will interpret a modification of the models built above based on the variables Age, EducLev3, Age* EducLev3, GenderFemale and EducLev3*GenderFemale.
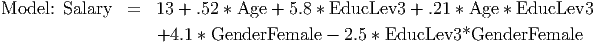
Interpretation: If GenderFemale = 0 and EducLev3 = 1, we have a male college graduate. Substituting these values in the model equation, we have
Salary = 13 + .52*Age + 5.8*1 + .21*Age* 1 + 4.1*0 - 2.5*1*0
Combining the constants and the Age terms, we have the equation for a male college graduate
Salary = 18.8 + .73*Age (3)
If GenderFemale = 1 and EducLev3 = 1, we have a female college graduate. Substituting these values in the model equation, we have
Salary = 13 + .52*Age + 5.8*1 + .21*Age* 1 + 4.1*1 - 2.5*1*1 (4)
In equation (4) we see that a female receives $4100 more than a male on the basis of gender alone. But she will receive $2500 less than a male if she has a college degree. Simplifying (4), we have the equation for a female college graduate:
Salary = 20.4 + .73*Age (5)
Comparing (3) and (5), we see that a female college graduate earns on the average of $1600 (20.4-18.8) more than a male college graduate. The difference is larger, however, for high school graduates (EducLev3 = 0). In this case, female high-school graduates earn $4100 a year more than male graduates. For example, comparing the salaries of 25-year old high school graduates, we have:
| Female: | Salary = 13 + .52 * 25 + 5.8 * 0 + .21 * 25 * 0 + 4.1 * 1 - 2.5 * 0 * 1 |
| = $30,100 | |
| Male: | Salary = 13 + .52 * 25 + 5.8 * 0 + .21 * 25 * 0 + 4.1 * 0 - 2.5 * 0 * 0 |
| = $26,000 | |
Example 10.7. Simplifying variables in the EnPact data
When we introduce interaction variables into the EnPact gender discrimination study, we find that
if we use the given variable names as they are found in C11 EnPact.xls [.rda] the software will
create interaction variable names that are too long to be completely viewed in its multiple
regression routine window. In addition, when we interact categorical variables with other variables,
particularly other categorical variables, the number of possible models from which we must find an
optimal model increases greatly, depending on the number of categories involved in creating the
interaction terms. There are situations, therefore, in which we have to not only shorten variable
names but also combine certain categories together in a meaningful way in order to reduce the
number of models we have to analyze. We illustrate how to do this with the EnPact data
spreadsheet: