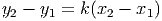
In the mathematical world and in the real world, most models are non-proportional.
- linear,
- logarithmic,
- exponential,
- square,
- square root, or
- reciprocal.
In general, a function is a mathematical object that takes an input, usually in the form of a number or a set of numbers, and gives an output number. (There are other types of functions possible, but we will concentrate on functions that satisfy this definition.) For a relationship between two variables, say x and y, to be a function, it must satisfy the following statement:
Every x-value must be associated with one and only one y-value.
This means that if you draw a graph of the function, and draw a vertical line through any point on the graph, that line will only touch the graph once. This is sometimes referred to as the vertical line test. Generally, if the variable y is a function of the variable x, we write y = f(x) to indicate this. If the variable y is a function of several variables (say x1, x2, x3) then we write y = f(x1,x2,x3).
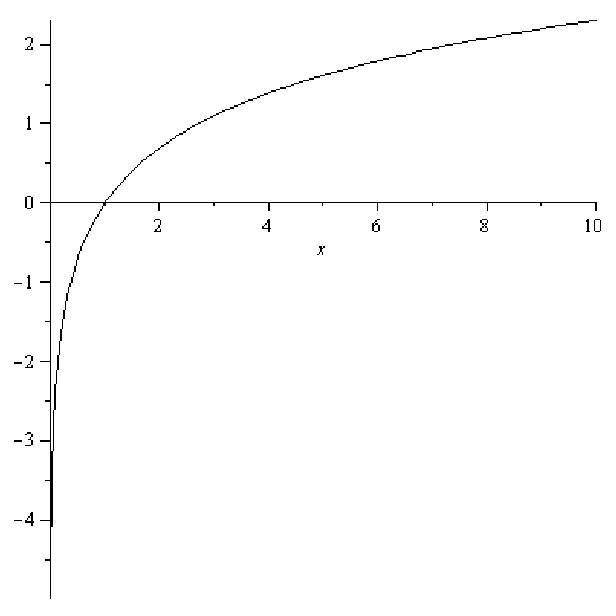
The natural logarithmic function has several important properties to note. The natural log of 0 is undefined; in other words ln(0) does not exist. If 0 < x < 1 then ln(x) < 0, and ln(1) = 0. This means that the point (1, 0) is common to all basic log functions. This is actually a restatement of the fact that any base raised to the zero power is equal to 1.
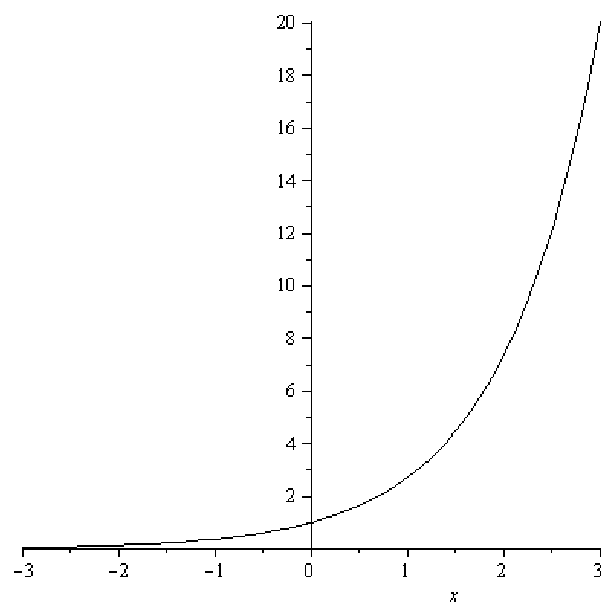
In addition, since any positive number, like e, raised to a negative power is a number between 0 and 1, we know that if -∞ < x < 0 then 0 < ex < 1. Since any number raised to the zero power is 1, we also know that e0 = 1 so the point (0, 1) is on the graph of all basic exponential functions.
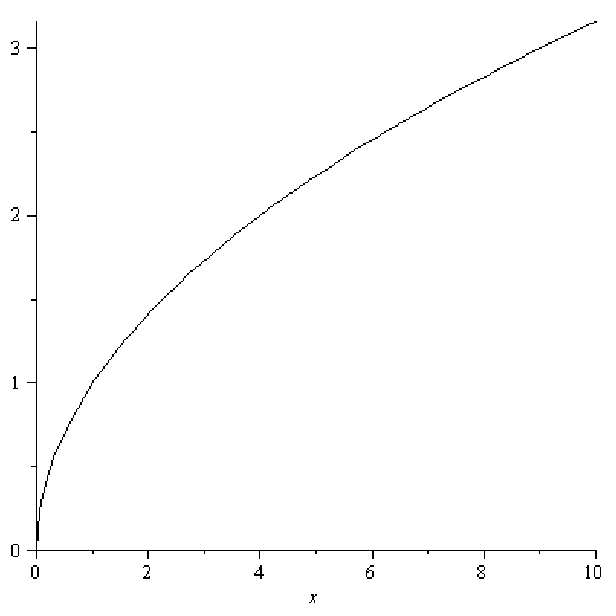
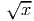 . Another way to write the function reminds us of its
relationship with the squaring function: y = x1∕2 = x0.5. (Read this as: y is x raised
to the one-half power or x to the 0.5 power.) The basic square root function is
concave down everywhere. In figuer 11.5, the square root function is not graphed for
values of x less than 0, since the square root of a negative number is an imaginary
quantity.
. Another way to write the function reminds us of its
relationship with the squaring function: y = x1∕2 = x0.5. (Read this as: y is x raised
to the one-half power or x to the 0.5 power.) The basic square root function is
concave down everywhere. In figuer 11.5, the square root function is not graphed for
values of x less than 0, since the square root of a negative number is an imaginary
quantity.
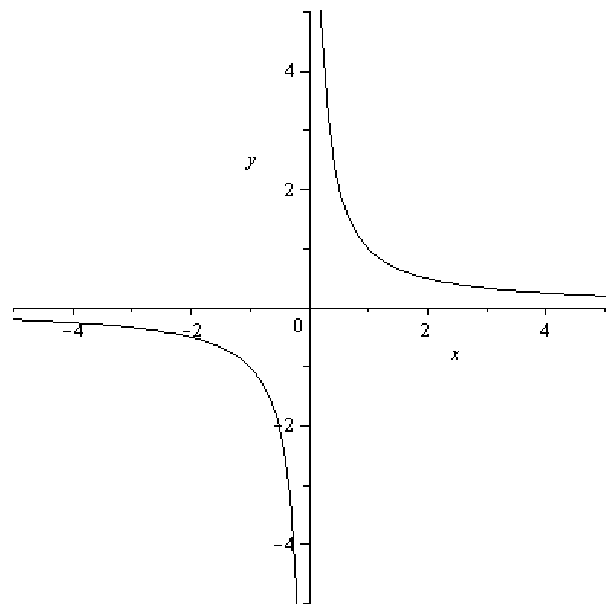
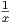 . This function also has an alternative form in which x is raised to a power:
y = x-1. Notice that the reciprocal function shown in figure 11.6 has several interesting
features: It has different concavity on the left and the right; it does not even exist at x = 0
since any number divided by zero is undefined; in fact, the reciprocal function never crosses
either axis.
. This function also has an alternative form in which x is raised to a power:
y = x-1. Notice that the reciprocal function shown in figure 11.6 has several interesting
features: It has different concavity on the left and the right; it does not even exist at x = 0
since any number divided by zero is undefined; in fact, the reciprocal function never crosses
either axis.
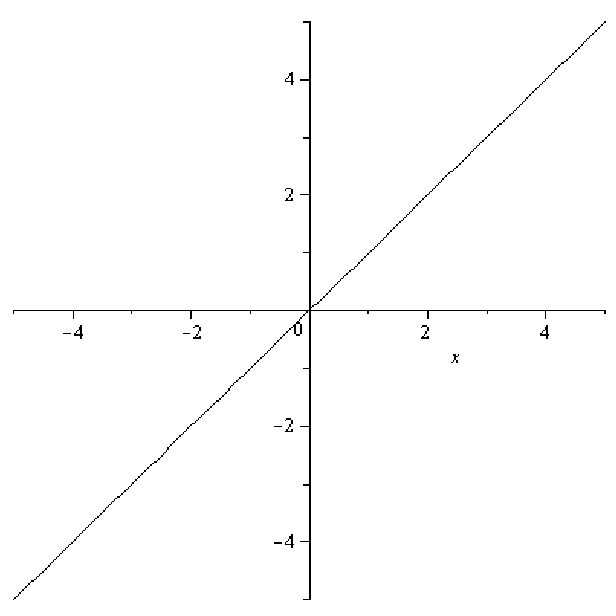
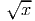 .
.
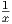 .
.