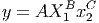
where A, B, and C are all constants (parameters).
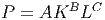
Notice that it is a multiplicative model as discussed above. There are some important cases in the Cobb-Douglas model depending on the values of the two powers, B and C. In general, these constants are both less than 1. The model reflects the idea that if you have a lot of labor investment (lots of workers) but not enough capital (equipment for the workers to use) then productivity is hampered. If you have a lot of capital (equipment for production) but not the labor to use it, then production also suffers.