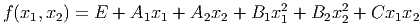
In this, we assume that at least one of the B coefficients is non-zero. Other texts may refer to the model in slightly different terms, but the important things to note are that (1) this is a polynomial model (in two variables) and (2) the degree of each term (sum of the powers of each variable) is either 0, 1 or 2. For example, the terms with a B coefficient all have one variable raised to the second power and the other raised to the zeroth power, so they are degree 2. The cross term (the term with the C coefficient that involves both independent variables) has both variables raised to the first power, so its degree is 1 + 1 = 2 as well.
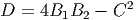
The shape of the graph (as we will see in the examples), depends on this quantity in the following ways:
- If D > 0 and B1 > 0, then the graph will look like a bowl.
- If D > 0 and B1 < 0, then the graph will look like a hill.
- If D < 0, then the graph will look like a saddle.
- If D = 0, then the discriminant is not helpful.
There are two other possible shapes for the graph, which occur if the coefficients in front of all instances of one variable are zero. In that case, the graph looks like either a trough (if the remaining B coefficient is positive) or a speed bump (if the coefficient is negative).
Depending on your viewpoint and the exact values of your graph, you may not be able to see it has a particular shape, though (see example 5).