Example 15.1. Derivative formula for logarithmic models
In example 1 we developed a model for the cost of electricity as a function of the number of units
of electricity produced. Marginal analysis can help us to make more specific sense of this model by
helping us to interpret how much each unit of electricity affects the total cost of producing the
electricity. The model had the form f(x) = A + B * ln(x):
Cost = -63,993.30 + 16,653.55 ⋅ Log(Units)
Suppose that we are currently producing 500 units of electricity. How much would it cost to produce one more unit of electricity? We can put this into a spreadsheet to compute it fairly easily. The results are shown below, and were obtained by setting up a formula for the difference quotient of the function, with a variable for h so that we can let h get very small. This lets us see what the instantaneous rate of change of the cost function is (this data is reproduced in the first worksheet of C15 LogDerivative.xls [.rda]).
| A | -63,993.30 | ||||
| B | 16,653.55 | ||||
| X | 500 | ||||
| H | X+H | F(X) | F(X+H) | DF = F(X+H)-F(X) | DF/H |
| 10 | 510 | 39501.99 | 39831.77 | 329.7840438 | 32.9784 |
| 1 | 501 | 39501.99 | 39535.26 | 33.27383724 | 33.27384 |
| 0.1 | 500.1 | 39501.99 | 39505.32 | 3.330376973 | 33.30377 |
| 0.01 | 500.01 | 39501.99 | 39502.32 | 0.333067669 | 33.30677 |
| 0.001 | 500.001 | 39501.99 | 39502.02 | 0.033307067 | 33.30707 |
From this, it seems that when current production is at 500 units, each additional unit of electricity will cost approximately $33.31. In contrast, if are currently producing 1,000 units of electricity, the marginal cost is about $16.65/unit.
| A | -63,993.30 | ||||
| B | 16,653.55 | ||||
| X | 1000 | ||||
| H | X+H | F(X) | F(X+H) | DF = F(X+H)-F(X) | DF/H |
| 10 | 1010 | 51045.35 | 51211.06 | 165.7083324 | 16.57083 |
| 1 | 1001 | 51045.35 | 51061.99 | 16.64522877 | 16.64523 |
| 0.1 | 1000.1 | 51045.35 | 51047.01 | 1.665271738 | 16.65272 |
| 0.01 | 1000.01 | 51045.35 | 51045.51 | 0.166534667 | 16.65347 |
| 0.001 | 1000.001 | 51045.35 | 51045.36 | 0.016653542 | 16.65354 |
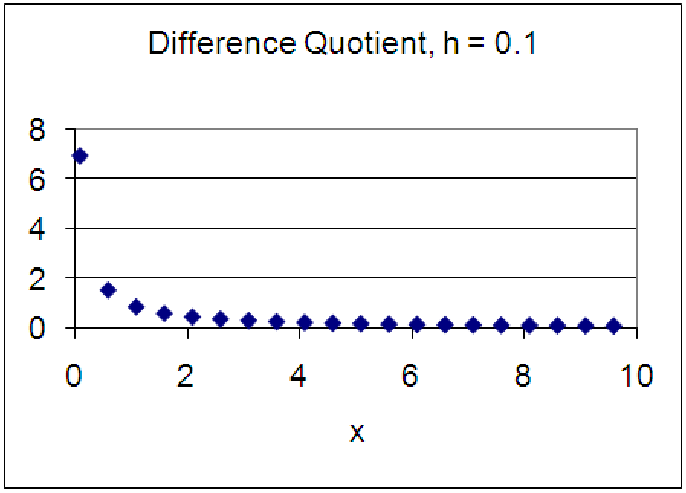
Now, what can this tell us about the derivative formula of a logarithmic function? Quite a lot, actually. Notice that as the production level increased (from 500 to 1000 units) the derivative (approximated by the column labeled ”DF/H”) decreased. Thus, we expect the derivative of a logarithmic function to be a decreasing function. This makes perfect sense when looking at the graph of a logarithmic function, since the graph ”flattens out” the farther you move along the x-axis. We can repeat the same method of analysis from chapter ?? to build a table of values for [ln(x)]′. If we plot these values, we get a graph much like the one below (see the second worksheet of Ch15 LogDerivative.xls [.rda]).
Notice that the difference quotient appears to be very similar to the inverse function, f(x) = x-1. This is a power function, so we can superimpose a trend line on this data using a power function. If we do, we find remarkable agreement, even with h = 0.1. Reducing h will, however, quickly achieve a nearly perfect fit for the inverse function to the difference quotient. While we have not truly proven this, we can assert with some confidence that
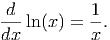
Now, we can use this along with what we already know about derivatives to determine the derivative of a more complete logarithmic model:
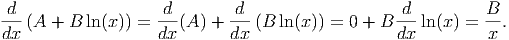
Thus, we expect that the derivative of the logarithmic function above (with A = -63, 993.30 and B = 16, 653.55) to be equal to B∕x = 16, 653.55∕x. So when the production level is 500, the derivative should be 16,653.55/500 = 33.3071, which is extremely close to the number we estimated using the difference quotient above. If the production level is 1000, we expect the derivative to be 16,653.55/1000 = 16.65355, which is again very close to the estimates determined earlier.
Example 15.2. Derivative of a logarithmic function
Find the derivative of the function f(x) = 3 - 2 ln(5x) with respect to the variable
SxS.
f′(x) = 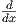 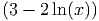 |
|
|
= 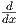 (2) + (2) + 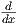 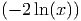 |
| Using the sum rule for derivatives |
= 0 - 2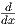 ln(5x) ln(5x) |
| Derivative of a constant is zero AND derivative of a constant times a function |
= -2 ⋅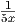 ⋅ ⋅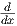 (5x) (5x) |
| Using the chain rule |
= -2 ⋅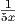 ⋅ 5 ⋅ 5 |
| Computing the derivative of the linear function |
= -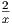 |
| Simplifying the derivative |
Example 15.3. A more complex derivative
Now for the hardest example yet. Find the derivative of the compound function below:
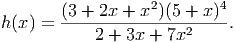
There are several different paths we could take through this problem. We’ll do it here by using the logarithmic derivative (one could use the chain, product and quotient rules all at once also). To do this, we take the natural logarithm of both sides and simplify the resulting mess that appears on the right hand side.
![[ ]
(3 +-2x-+-x2)(5-+-x-)4-
ln(h (x)) = ln 2 + 3x + 7x2
2 4 2
= ln(3 + 2x + x ) + ln(5 + x ) - ln(2 + 3x + 7x )
= ln(3 + 2x + x2) + 4ln(5 + x) - ln (2 + 3x + 7x2 )](Text_Fall_2014306x.png)
Taking the derivative is now a matter of using the chain rule, piece by piece. For example, we know that the derivative of the left hand side with respect to the variable x is just h′(x)∕h(x), where h′(x) is the derivative we really want. Now we need to take the derivative of the right hand side; we’ll do it in three parts, one for each term on the right hand side.
![-d-ln(3 + 2x + x2) = -----1------⋅-d-(3 + 2x + x2 ) = --2-+-2x----
dx 3 + 2x + x2 dx 3 + 2x + x2
d d 1 d 4
---[4ln(5 + x)] = 4 ⋅---ln(5 + x) = 4 ⋅------⋅---(5 + x) = ------
dx dx 5 + x dx 5 + x
-d-ln(2 + 3x + 7x2) = -----1-------⋅-d-(2 + 3x + 7x2) = --3-+-14x----
dx 2 + 3x + 7x2 dx 2 + 3x + 7x2](Text_Fall_2014307x.png)
Now we can put this all together to get
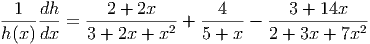
Cross multiplying by h(x) then gives us the derivative of h with respect to x
![dh [ 2 + 2x 4 3 + 14x ] (3 + 2x + x2)(5 + x)4
---= ------------+ ------- ------------- ⋅ ---------------------
dx 3 + 2x + x2 5 + x 2 + 3x + 7x2 2 + 3x + 7x2](Text_Fall_2014309x.png)
After a great deal of work, this can simplify to
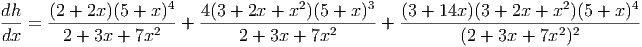
If we get a common denominator, we can further simplify this, but it doesn’t really help.