Vector Valued Functions

The functions we have discussed so far are all scalar functions since they return a singe, scalar value. However, many scientific and engineering applications require the use of vector valued functions which return, instead of a scalar, a vector. Often, they are called vector fields. For example, the velocity field of a fluid or the electro-magnetic field of a distribution of charges are both vector fields. The idea of a scalar function is that every point in the domain is associated to a real number in the range. In the case of a vector field, each point in the domain (usually three dimensional space) is associated to a three-dimensional vector. This can be done in any number of dimensions, but it is easiest to picture in two dimensions.

Usually we denote a vector valued function in two ways. First, we write the name of the function in capital letters. Second, we put a vector arrow on top of the name of the function. Thus, $\vec{F}(x,y)$ is a vector valued function, while f(x,y) is not.

For example, the vector field $\vec{G}(x,y) = x\hat{i} + \hat{j}$associates the vector $x\hat{i} + \hat{j}$ to every point (x,y) in the plane. At the point (0,0), the vector field has the value $\hat{j}$. At (1,-1) the vector field is $\hat{i} + \hat{j}$, and so forth. A graphical representation is more helpful.

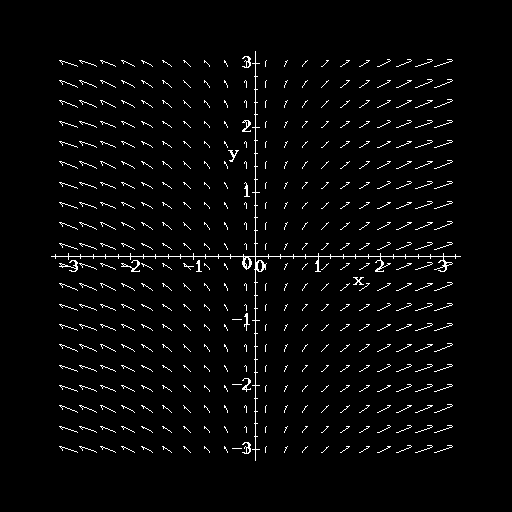
We can have vector fields in three space, although these are more difficult to draw than even a surface plot of a function.

One other notation that you will frequently encounter involves the position vector, $\vec{r}$, of a point (x,y,z). The position vector is $\vec{r} = x\hat{i} + y\hat{j} + z\hat{k}$. The magnitude of this vector is denoted r and has the value $r = \vert\vert \vec{r} \vert\vert = \sqrt{x^2 + y^2 + z^2}$.Usually, we denote vector fields as $\vec{F}(\vec{r})$ rather than $\vec{F}(x,y,z)$. For example, the vector field $\vec{F}(\vec{r}) = \vec{r}/r^3$ has magnitude

$$\vert\vert\vec{F}\vert\vert = \frac{\vert\vert\vec{r}\vert\vert}{r^3} = \frac{r}{r^3} = \frac{1}{r^2}$$

at each point in three space. Since the vector is simply a multiple of the position vector, at each point in space the vector field points directly away from the origin. The magnitude drops off as 1/r² or rather, the inverse-square of distance.

When it comes to three dimensional vector fields, the two most important details for getting a handle on what is happening are the magnitude and direction of the field. Magnitude is easy to compute (as shown above.) Direction is usually a bit harder to ascertain. As is clear(?) from the following graph of the vector field above.

For a second example, consider the vector field $\vec{G}(\vec{r}) = -2\vec{r}/r$. The magnitude of this field is equal to 2 everywhere. Thus, it is constant. It's direction is antiparallel to the position vector, so it always points toward the origin. Note however that the vector field is not defined at the origin (as in the previous example) since, at (0,0,0) the magnitude of the position vector is which means the vector field would have the value of $\vec{0}/0$ which is undefined.