


Next: What does a linear
Up: Linear Functions-Planes
Previous: Linear Functions-Planes
The word linear relates to lines. In one variable, say x, a linear
function has
the familiar form y = mx + b. It's graph is a line with slope m and a
y-intercept of b. A linear function of n variables, say 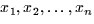 , a linear function has the form
, a linear function has the form
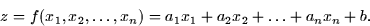
The constants 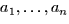 are the slopes of the function in each
direction. Thus, if we fix all the variables except x1 and then change
x1 by one unit, the total change in z will be
are the slopes of the function in each
direction. Thus, if we fix all the variables except x1 and then change
x1 by one unit, the total change in z will be 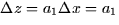 . Notice that, as in the one variable case, each variable appears
only to the first power in a polynomial. No other functional dependence on
the variables is allowed if the function is to be linear. We cannot have
cross terms either, like x1 x2.
. Notice that, as in the one variable case, each variable appears
only to the first power in a polynomial. No other functional dependence on
the variables is allowed if the function is to be linear. We cannot have
cross terms either, like x1 x2.
Vector Calculus
1/8/1998
![]() , a linear function has the form
, a linear function has the form
![]()