What does a linear function look like?

For now, let's concentrate on linear functions of two variables in the form

z = mx + ny + b.

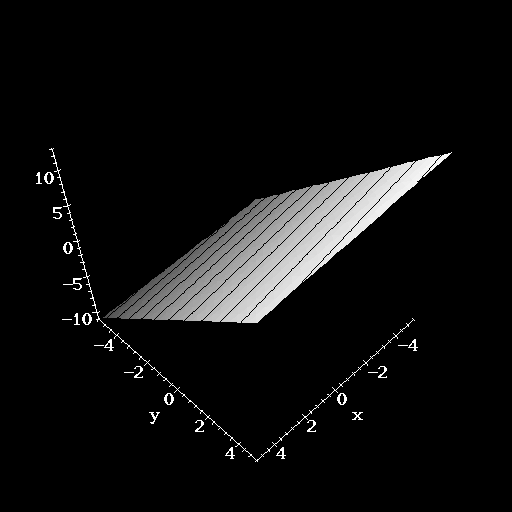
To picture this, start with the sections. If we fix x = c the sections look like z = ny + (mc + b). These are straight lines in the yz-plane with a slope of n and z-intercept of mc+b. Similarly, the sections with y = c are straight lines in the xz-plane with slope m and z-intercept nc + b.

(sections of a plane in x and y: z = -(1/3)x + 2y + 1)

What about the contour diagram for a plane? Setting z = c gives us the graph of $c = mx + ny + b \Rightarrow y = -(m/n)x + (c-b)/n$. These are straight lines in the xy-plane with slope -m/n and y-intercept of (c-b)/n.

Putting all of this together, we have a function whose sections in x are parallel lines of slope n, whose sections in y are parallel lines of a different slope, m, and whose contours are parallel lines with a slope -m/n. What kind of surface will this form?