Example 1. Compute the curl of ![]() .
.
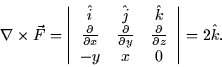 |
(5) |
This is the vector field on the left in the figure above. As you
can see, the analytical approach does bear out that the curl has positive
![]() component.
component.
Example 2. Compute the curl of ![]() . Now,
. Now, ![]() so
so
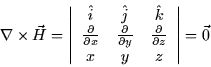 |
(6) |
This is, as you have no doubt guessed, the vector field on the far right in the above illustration.