What does it mean to ``Optimize Subject to a Constraint''?

When we optimize a function f(x,y) subject to a constraint, say $g(x,y) \le c$ we must consider two possibilities.

1.

The optimum point lies inside the region of the xy plane defined by $g(x,y) \le c$, or

2.

The optimum point lies on the boundary of the region.

This may seem painfully obvious, but the reason for separating the two cases is that there is a very different technique for finding the optimum values in each case.

In case (1), we are essentially performing an unconstrained optimization, as in the previous sections. The only difference is that, if we find an extrema of f(x,y) that is outside the region, we simply ignore it.

Case (2) is very different. We are no longer considering the whole domain of f(x,y) but only the boundary of our constraint. What does it mean to have a maximum or minimum here? Look at the graph below. It shows level curves of z = f(x,y) as well as the curve g(x,y) = c.

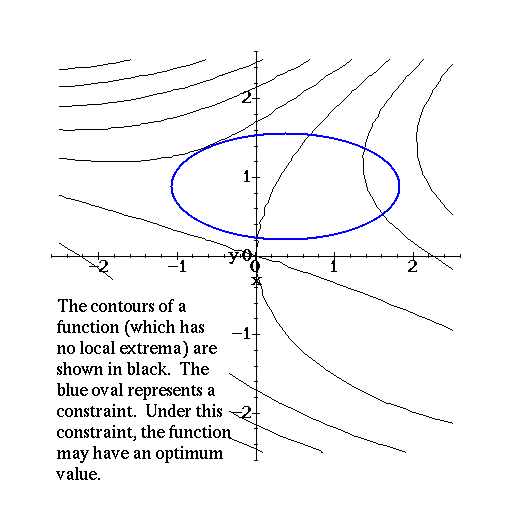
Suppose we start at the point labeled A. Here, $\mbox{grad}f$ has a component along the direction of the constraint curve (recall that the gradient is perpendicular to the level curves.) Thus, by moving along the constraint in this direction we can increase the value of the function. This means that point A is not the maximum. A similar situation occurs at point B. Moving to point C we find that the gradient of f is now perpendicular to the constraint curve as well. Thus, we cannot increase f by moving along the constraint. If we did move on to point D, we would find the gradient of f pointing back in the direction of C.

Notice also that if we take the constraint g(x,y) = c as a level curve of the function z = g(x,y), then at point C, the gradients of f and g are parallel. So, at the optimum point on the boundary of the constraint region, we have

$$\mbox{grad}f = \lambda \mbox{grad}g.$$ (10)

This vector equation is the basis for locating extrema of constrained functions.

Click here to view an animation of the process of using the gradients to search for the constrained optimum. To return here, simply close the new window which opens.