Setting up the Equations and Putting it Together

To summarize finding constrained extrema for f(x,y) subject to 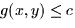$g(x,y) \le c$:

1.

Find all local extrema inside the region $g(x,y) \le c$.

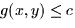2.

Find all triplets 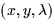$(x,y,\lambda)$ such that both

(a)

g(x,y) = c, and

(b)

$\mbox{grad}f = \lambda \mbox{grad}g$

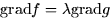
are met. Note that this is really three equations, one from (a), and two from each of the components of the vector equation in (b).

3.

Compute the value of f(x,y) at each of the optimum points obtained from (1) and (2). Compare these values to choose the maximum and the minimum.

The parameter 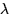$\lambda$ is called the Lagrange multiplier and the process of optimizing f subject to a constraint is often called the Lagrange multiplier method.