


Next: Interpretation of the Lagrange
Up: Applications of Derivatives
Previous: Setting up the Equations
Find the maximum of the function f(x,y) = x2 - y subject to the
constraint that 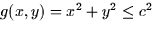 .
.
- 1.
- Inside the circular constraint region,
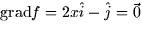 gives an entire line of critical points: (0, y) where
gives an entire line of critical points: (0, y) where
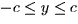 since we must stay inside the region.
since we must stay inside the region.
- 2.
- On the boundary, we must solve the equations
|  |
(11) |
These can be reformulated as
| 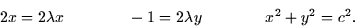 |
(12) |
The leftmost equation says that 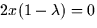 which admits two
solutions, x = 0 and
which admits two
solutions, x = 0 and  .If we take x = 0 the third equation gives
.If we take x = 0 the third equation gives 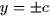 and the then we
have
and the then we
have 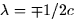 .
.
If we take  the second equation gives y = -1/2 and the third
then gives us that
the second equation gives y = -1/2 and the third
then gives us that 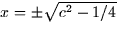 .
.
Thus we have located four critical points on the boundary
|  |
(13) |
- 3.
- We now compute the value of f at each critical point.
- (a)
- f(0,y) = -y. Since this critical point must lie inside the region,
we know that -y lies between -c and +c.
- (b)
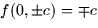
- (c)
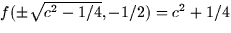
Thus, the maxima are clearly the points 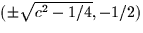 .
.




Next: Interpretation of the Lagrange
Up: Applications of Derivatives
Previous: Setting up the Equations
Vector Calculus
12/6/1997
![]() .
.![]() the second equation gives y = -1/2 and the third
then gives us that
the second equation gives y = -1/2 and the third
then gives us that ![]() .
.