If y = ax + b, then it is easy to see that y is changing with respect
to x. How fast is it changing? Since y is a straight line, we know
that 
slope of the straight line = a, so for
every unit x increases, y increases by a units.
What about a function like 
? It doesn't have a constant slope.
In fact, as x gets larger, it looks like the slope increases as well.
One of the two main components of calculus is the computation of the slopes
of such functions. Since the slope changes as x changes, it is
reasonable to assume that the slope is really a function of x. This
slope function will output the slope of a line that is tangent to the
function at each value of x. This function is called the derivative,
since it is a function that is derived from (based on) another function.
The derivative of the function y = f(x) is denoted in many ways. Among
them are y', dy/dx, and df(x)/dx.
To define the derivative, we will pretend that the function f(x) is a straight line, and use our knowledge about the slopes of lines in order to develop the notion of the derivative. Suppose we want to know the derivative of f at the point (x, f(x)). Let's draw a straight line between the point (x, f(x)) and a nearby point (x + h, f(x+h)). This line is called the secant line.
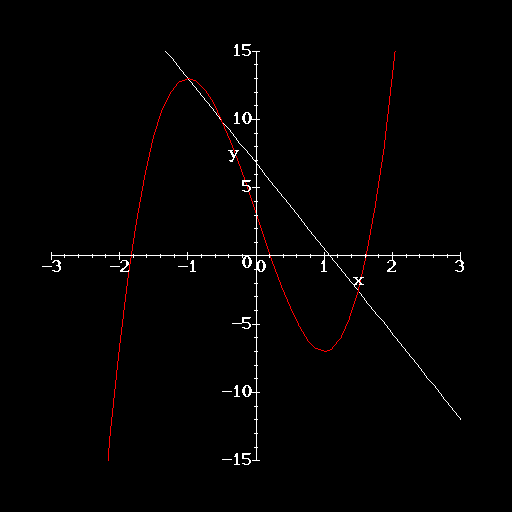
The slope of this secant line will be
Notice what happens as 
. The end points of the
secant line get closer together and the line eventually becomes a better
and better approximation of the tangent line to the curve y = f(x) at the
point (x, f(x)). The slope of this tangent line is the slope of f(x)
at the point, in other words, it's the derivative.
Click here to view animation of this in another window. To return here, simply close the new window.
Thus the tangent line and the function have the same ``instantaneous slope'' at the point. This leads to the definition of the derivative.
