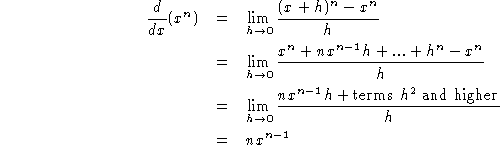The definition of the derivative is often cumbersome to work with. For
example, to compute the derivative of 
:
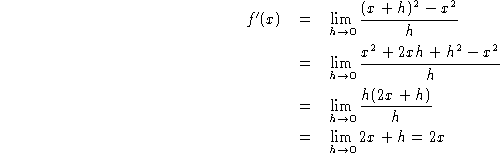
Imagine using the definition to compute the derivative of 
! This is not a task I (or anyone else) would relish.
However, the definition of the derivative can be used to prove a variety of facts, properties and rules about differentiation. The following is a quick list of important rules.
, if a is a real number.
Together, the first two properties show that the derivative is a
linear operation on functions that are differentiable. For a function to
be differentiable at 
, the function must be continuous at . That is,
Also, 
must not be a corner or strange kink (eg. f(x) =
|x| has a corner at x = 0.) In other words, as we take the limit in the
definition of the derivative, it must exist from the left and the right and
be equal (from both directions) to the slope of the function at that
point. This means that
Some of the more important (and frequently encountered) derivatives are shown below.
. This can be seen from
