Application of Derivatives: Computing Local Extrema

Now lets put all this stuff to use by utilizing derivatives to locate all of the local maxima and minima of a function. A local maxima is a point (x,f(x)) such that, for any point that is sufficiently close to x, the condition is satisfied. Thus, locally, the point (x, f(x)) is the highest point. Similarly, a local minima is a point which is lower than the surrounding points. To locate extrema such as these, we use our knowledge of derivatives. If a point (x, f(x)) is the maximum of f(x), then f'(x) = 0. If this were not true, then the slope would be either positive or negative, and by moving forward in x (or backward if the slope is negative) we could reach a higher point on the function since the slope is nonzero. This also holds for a point which is a minimum.

There is one sticky point, though. The derivative can be zero at a point that is not a maximum or a minimum. Thus, f'(x) = 0 is a necessary, but not sufficient condition for the point (x, f(x)) to be a local max or min. We can use the second derivative to help. If the function is concave up at the point where the derivative is zero, then the point must be a minimum. If the function is concave down, it is a maximum. If the second derivative is zero, then we have an inflection point.

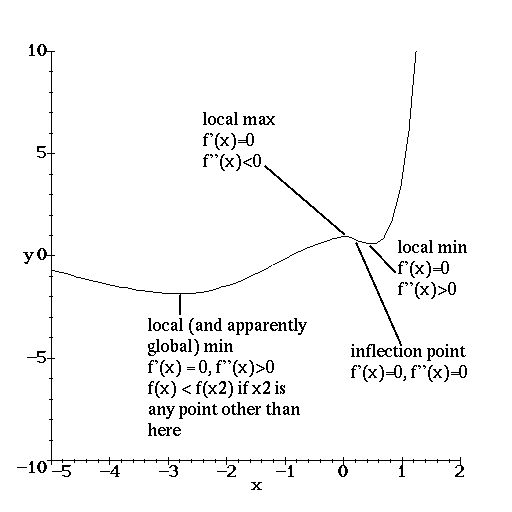
Consider the function

We will now calculate the local extrema.

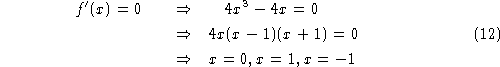
1. Calculate the first derivative, using the chain rule:

   

2. Locate all critical points of f(x) where f'(x) = 0:

   

3. Calculate the second derivative, using the product and chain rules:

   

4. Determine the concavity at each critical point:
   1. At the point (0, 1):

      

   2. At the point :

      

   3. At the point :