Since the derivative of a function is, in general, a function, we can also
take derivatives of the derivative, and so forth. The derivative of the
derivative is called the second derivative, and is denoted by 
and so on. Third derivatives and higher can also be taken.
Usually, the 
derivative of f(x) is denoted by 
if
.
For example, if 
, then 
and 
. Higher derivatives are 
, 
and
so forth.
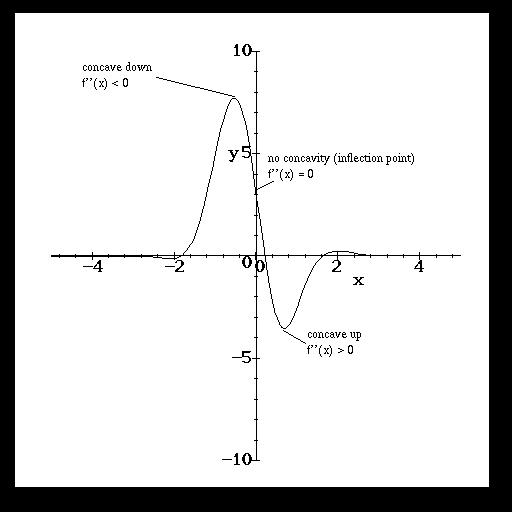
Interpretation of higher order derivatives is not always obvious. The first derivative represents the rate of change of a function with respect to the independent variable, or the slope. Thus the derivative of the position function for an object would be the object's speed. The second derivative is the rate of change of the first derivative. In the case where f(t) represents the position of an object, f''(t) is the objects acceleration.
More generally, the second derivative of a function at a point tells you the concavity of the function. A positive value of the second derivative indicates that function is concave up at that point, which means that it looks sort of like an upward opening parabola. A negative value for the second derivative indicates that the function is concave down, and looks like an upside down parabola.
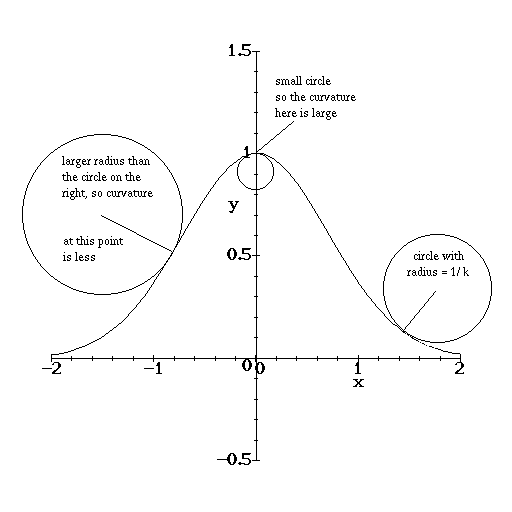
One other use for the second derivative is computing the curvature of a
function. Suppose y = f(x) describes some curve in the xy-plane. At
any point (x, f(x)) the curvature is defined to be the reciprocal of the
radius of the largest circle that can be made tangent to the curve at that
point. It can be computed by the formula
