Directional Derivatives

Now, $\frac{\partial f}{\partial x}$ and $\frac{\partial f}{\partial y}$ tell us how rapidly the function f(x,y) changes in the x and y directions. But suppose we don't want to be restricted to just moving in the x and y directions. For example, if the function f(x,y) represents the density of oil in an oil spill, and we are sitting in a boat in the center trying to clean the spill, we want to move toward the greatest concentration of oil. This might not be along the x or y axis. We could get there more rapidly if we knew how to compute the rate of change of the function in an arbitrary direction.

Thus, if we sit at the point (x₀,y₀) and move along the unit vector $\hat{u} = u_1\hat{i} + u_2\hat{j}$ how rapidly does the concentration (ie. the value of f(x,y)) change? Clearly, if $\hat{u} = \hat{i}$(ie. u₁ = 1, u₂ = 0) then the rate of change is $\frac{\partial f}{\partial x}$ since we are moving in the x direction. Also clear is that if $\hat{u} = \hat{j}$then the rate of change is $\frac{\partial f}{\partial y}$. What if we don't choose one of these special values though?

The directional derivative of f(x,y) in the direction of the unit vector $\hat{u} = u_1\hat{i} + u_2\hat{j}$ is

$$f_{\hat{u}} = \left(\frac{\partial f}{\partial x} \right)u_1 + \left(\frac{\partial f}{\partial y} \right)u_2.$$

It is easy to verify that in the special cases above, the correct value is obtained.

Note that the directional derivative relies on a vector to give a direction, but is itself a scalar quantity. All it tells us is how rapidly the function changes in the $\hat{u}$ direction. This is the reason for the notation $f_{\hat{u}}$: to emphasize the similarity between the direction derivative and the partial derivatives f_x and f_y. If we think of the quantity as a dot product

$$f_{\hat{u}} = \hat{u} \cdot \left( \frac{\partial f}{\partial x}\hat{i} + \frac{\partial f}{\partial y} \hat{j} \right)$$

then we again emphasize the scalar nature of the directional derivative. We'll speak more about the vector $\frac{\partial f}{\partial x}\hat{i} + \frac{\partial f}{\partial y}\hat{j}$later.

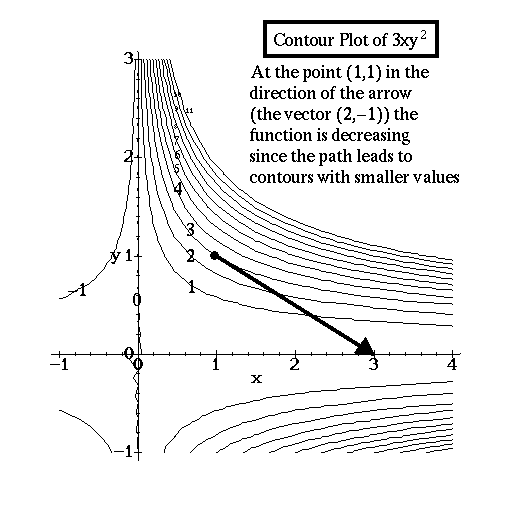
As an example, suppose we want to know the rate of change of f(x,y) = 3xy² at the point (1,1) in the direction of the point (3,0).

1.

We first compute the vector $\frac{\partial f}{\partial x}\hat{i} + \frac{\partial f}{\partial y}\hat{j}$at the point (1,1). Since f_x = 3y² and f_y = 6xy we find that the vector in question is $3\hat{i} + 6\hat{j}$.

2.

We now compute the vector $\hat{u}$. The displacement vector from (1,1) to (3,0) is $\vec{u} = (3-1)\hat{i} + (0-1)\hat{j} = 2\hat{i} - \hat{j}$. As a unit vector, this is $\hat{u} = (1/\sqrt{5})(2\hat{i} - \hat{j})$.

3.

We are now ready to calculate $f_{\hat{u}}$. Using the formula $f_{\hat{u}} = \hat{u} \cdot (f_x \hat{i} + f_y \hat{j}) = (1/\sqrt{5})(2\hat{i} - \hat{j}) \cdot (3\hat{i} + 6\hat{j}) = 0.$

This tells us that in that particular direction, the function is constant. The only way this can happen is if $\hat{u}$ actually points along one of the contours of the function at the point (1,1).