Let's look more closely at the formula for the directional derivative of
f(x,y) along the unit vector ![]() :
:
![]()
![]()
Thus, it is seen that the vector ![]() points toward
the largest increase in f(x,y) and has a magnitude equal to the rate of
change in that direction. The vector
points toward
the largest increase in f(x,y) and has a magnitude equal to the rate of
change in that direction. The vector ![]() is called
the gradient vector and is denoted by grad f. A quick computation
shows that for the function g(x,y) = 2x2 + 3xy + 4y2, grad
is called
the gradient vector and is denoted by grad f. A quick computation
shows that for the function g(x,y) = 2x2 + 3xy + 4y2, grad ![]() .
.
Graphically, the gradient is easy to find and interpret. If you are
looking at the surface plot of a function, the gradient at a point always
points toward the highest nearby point. If you are looking at a contour
diagram, the gradient is always perpendicular to the contours. This is
easy to understand. If we move along a contour, the rate of change of f
is zero since we are remaining at a fixed value of z = f(x,y). Thus,
unless grad ![]() along the contour, the angle between grad f
and the direction of greatest increase of f must be 90 degrees so that
the cosine factor in the dot product for directional derivative will be
zero. If this is true, then the gradient must point 90 degrees away from
the contour.
along the contour, the angle between grad f
and the direction of greatest increase of f must be 90 degrees so that
the cosine factor in the dot product for directional derivative will be
zero. If this is true, then the gradient must point 90 degrees away from
the contour.
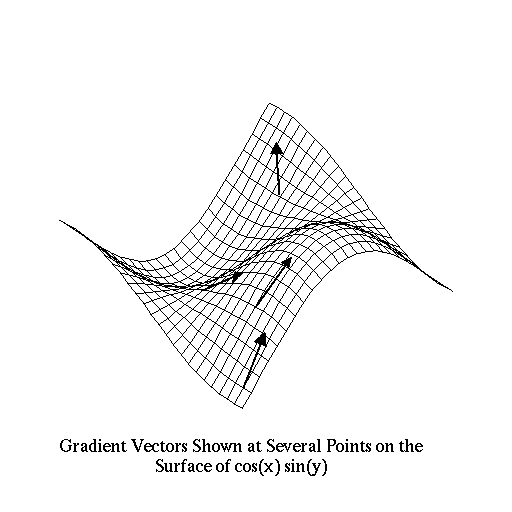
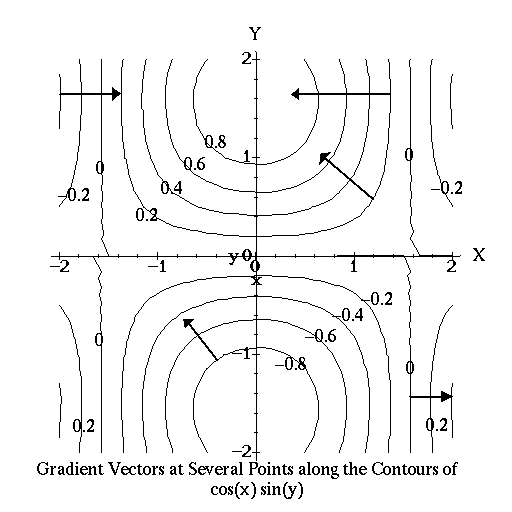
Note that the gradient is a vector quantity. The directional derivative is a scalar. As a vector, the gradient of a function has a magnitude and direction. It points toward the greatest increase in the function and has a magnitude equal to the increase in that direction. The directional derivative and the gradient are related by the following formula:
![]()
In order to find the maximum rate of increase of f(x,y) at a point, simply compute the gradient and calculate the magnitude. To find the greatest rate of decrease at a point, move along the direction of -grad f.