The Chain Rule

The chain rule should be familiar from one variable calculus. It's a way of determining the derivative of a function with respect to a variable when that variable depends on another variable and so on. Suppose that V(r) gives the volume of a spherical balloon based on its radius, r. Now, if the balloon is being inflated, r is also a function of time, r(t). Thus, indirectly, V is also a function of t: V(r(t)). To find dV/dt we simply string together all the derivatives which connect V to t:

$$\frac{dV}{dt} = \frac{dV}{dr} \frac{dr}{dt}.$$

The same chain of functional dependencies can happen in multivariable calculus. One common example is as follows. Let f(x,y) be a function of two variables. In polar coordinates, $x = r\cos \theta, y = r\sin \theta$. Thus, the function f depends on both r and $\theta$indirectly. To compute $\frac{\partial f}{\partial r}$ or $\frac{\partial f}{\partial \theta}$ we need to include all of the possible dependencies:

$$\frac{\partial f}{\partial r} = \frac{\partial f}{\partial x... ...ial f}{\partial x} + \sin \theta \frac{\partial f}{\partial y}.$$

Notice that if you think of each term above as fractions and cancel all common factors, you'll get $\frac{\partial f}{\partial r} = \frac{\partial f}{\partial r} + \frac{\partial f}{\partial r}$. No matter how complicated the dependence, this should always happen, even though it's not technically accurate to cancel the common factors in such an expression. Further,

$$\frac{\partial f}{\partial \theta} = \frac{\partial f}{\part... ...al f}{\partial x} + r\cos \theta \frac{\partial f}{\partial y}.$$

Let's try a more complex example. Suppose we have a function of three variables: w = w(x,y,z). Now, suppose x, y, and z all depend on the two variable s and t. That is, x = x(s,t), y = y(s,t), and z = z(s,t). Further, suppose that s = s(u,v) and t = t(u,v). What are dw/du and dw/dv?

To answer this, it's easiest to use a sort of tree diagram. Each level of the tree is one level of functions. The branches that feed into each node show how that variable depends on the variables below it. To construct the correct chain of derivatives, start at the top of the tree. The first factor of the first term is the derivative of the variable at the top level with respect to the variable at the next level down. The next factor in the first term is the derivative formed from the next level and so on. Once you get down to the variable you need, stop, and start at the top forming the second term by branching down appropriately.

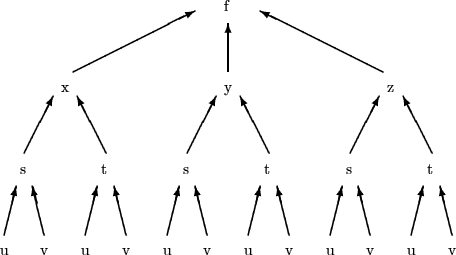
In this example, we see that

$$\frac{\partial w}{\partial u} = \frac{\partial w}{\partial x... ... z} \frac{\partial z}{\partial t} \frac{\partial t}{\partial u}$$

and

$$\frac{\partial w}{\partial v} = \frac{\partial w}{\partial x... ...z} \frac{\partial z}{\partial t} \frac{\partial t}{\partial v}.$$

As you can no doubt see, it is easy for this to become quite complicated. The tree diagram will help you straighten out what is happening.