


Next: The flux Integral
Up: Flux Integrals
Previous: Flux Integrals
Return to Block Three menu.
Return to Main Menu.
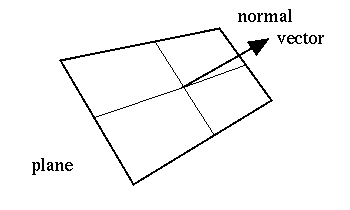
A surface is said to be oriented (when this is possible) if a direction of
positive flow has been chosen. To choose a direction of positive flow we
specify a normal vector to the surface. Any flow that is in the general
direction of the normal vector is considered positive and any flow which
heads against the normal vector is considered negative. Note not all
surfaces are orientable (e.g. the Möbius band)
Examples:
- 1.
- The plane z=0 (the xy plane) has two possible orientations, up or
down. Every normal vector looks like
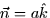 . If a is positive
then the normal points up and if a is negative then the normal points
down. As an example consider the upward normal
. If a is positive
then the normal points up and if a is negative then the normal points
down. As an example consider the upward normal 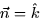 .
We can simplify our lives a little by always using unit normal vectors. If
we do this then there are only two choices for the normal vector, up or down.
.
We can simplify our lives a little by always using unit normal vectors. If
we do this then there are only two choices for the normal vector, up or down.
- 2.
- Consider the sphere x2+y2+z2=1. For closed surfaces we
usually take the normal vector to point outwards. In this case a vector that
points radially outward will be a normal vector.

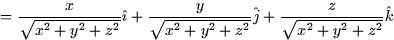
and any flow out of the sphere is considered positive while flow into the
sphere is considered negative.



Next: The flux Integral
Up: Flux Integrals
Previous: Flux Integrals
Vector Calculus
8/21/1998

![]()
![]()

![]()
![]()