Example 2: Flux Through A Surface with Two Boundaries

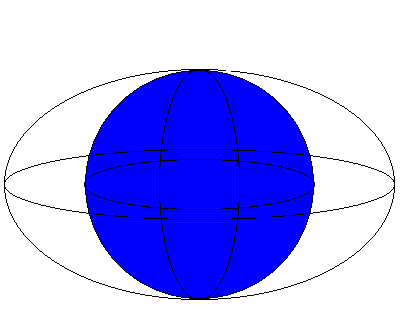
First of all, what do we mean by a region with two boundaries? Here's an example. Let S₁ be the sphere of radius 1 centered at the origin and let S₂ be the ellipsoid x² + y² + 4z² = 16, both oriented outward.

Clearly, S₂ contains S₁. Let's call the solid region in between them W. W has two boundaries: S₂ is its outer boundary and S₁ is the inner boundary. To calculate the total flux out of the region W we need the flux through both of these surfaces. But watch out! Since ``out of W'' points in the opposite direction of the orientation of S₁, we need to subtract the flux through S₁ from the flux through S₂:

$$\mbox{Total flux out of }W = \int_{S_2} \vec{F} \cdot \hat{n}dS - \int_{S_1} \vec{F} \cdot \hat{n}dS.$$

For a good example of an application of this using the divergence theorem, check out problem 9 on the fall 1996 final exam.