Integration in Two Variables
by Riemann Sums

Suppose we have a rectangular region of a city that is one mile by 2 miles and we want to know the total population of this region from the population density. One way to do this is to break the region into blocks, let's say 0.2 miles by 0.4 miles, and look at the population density in each block. The following table shows this, where the density is measured in $(\mbox{hundreds of people})/(\mbox{mile})^2$.

y / x 0.2 0.4 0.6 0.8 1.0

0.4 5 6 10 8 8

0.8 6 8 12 8 7

1.2 4 8 10 9 7

1.6 3 5 7 6 5

2.0 2 3 4 3 4

To get the total population in one block, we simply multiply the density by the area of the block, where $\mbox{area} = 0.2 \times 0.4 \thinspace \mbox{mile}^2 = 0.08 \thinspace \mbox{mile}^2$. Adding the population of all the blocks then gives us the total population. We find that

$$\mbox{Total pop} = (5 + 6 + 10 + 8 + \dots + 4 + 3 + 4) (0.08)$$

$$= 12.64 \quad \mbox{hundred people} = 1,264 \quad \mbox{people}.$$

Note that this is just an estimate of the number of people. We've assumed that over a block, the population density is constant and only varies from block to block. This is usually not the case. To get a better estimate, we'd have to break the region up into more blocks (that are smaller) and repeat the process.

Basically, we've taken a function of two variables f(x,y) (in this case f gives the population density at the point (x,y) ) and integrated it over the region. We did this using a Riemann sum. Here's a slightly more detailed, but abstract, picture of what we're doing.

Let f(x,y) be defined on a rectangular region, R, which is given by $a \le x \le b, c \le y \le d$. Break this region into small, but equally spaced blocks measuring a constant $\Delta x$ in the x direction and $\Delta y$ in the y direction.

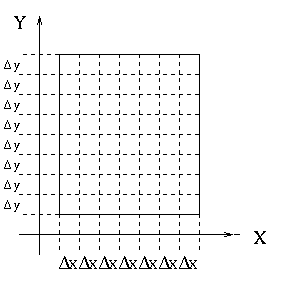
The area of each block is a small piece of the total area of R: $\Delta A = \Delta x \Delta y$. To get the Riemann sum for the integral of f over R, we evaluate f at a point in each of the blocks, multiply this by $\Delta A$, and add this to the result of all the other blocks. To make it easy, we'll evaluate f at the lower left corner of each block. The Riemann sum can then be written as

$$\sum_{i,j} f(x_i, y_j)\Delta x \Delta y.$$

This sum is a rough estimate of the definite double integral of f over R which is written

$$\int_R f dA.$$

Remember, this is only an estimate because we are assuming that f is constant over each of the blocks. To be accurate, we should take the limit as the blocks get smaller and smaller (as their number goes to infinity). Thus,

$$\int_R f dA = \lim_{\Delta x, \Delta y \rightarrow 0} \sum_{i,j} f(x_i,y_j)\Delta x \Delta y.$$