


Next: Integration Over Non-Rectangular Regions
Up: Integration in Several Variables
Previous: Integration in Two Variablesby
The Riemann sum above is actually two sums, one in i and one in j:
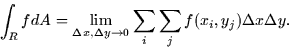
This is very similar to the way we do integrals in one variable:
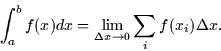
We could apply this to the two variable case by breaking up the summation
and the limits, as follows:
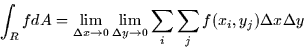
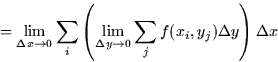
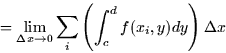
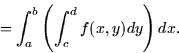
This gives a clue as to how we should go about evaluating the double
integral. We do it one variable at a time (surprise!) This type of
integral is called an iterated integral since we integrate with
respect to one variable and then another. As it turns out, we could have
organized the summations differently and reversed the order of integration:
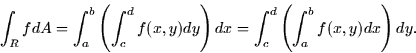
Usually, reversing the order will take more work, but for a rectangular
region such as this, it's pretty straightforward.
Here's an example: Integrate the function f(x,y) = x2 + 2xy + y2 over
the rectangle, R, given by 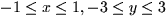 .
.
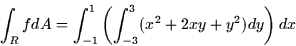
![\begin{displaymath}
= \int_{-1}^1 \left[ x^2y + xy^2 + \frac{1}{3}y^3 \right]_{-3}^3 dx \end{displaymath}](img22.gif)
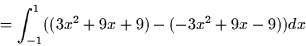
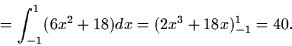
We could also evaluate this by integrating in the opposite order:
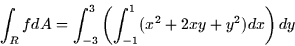
![\begin{displaymath}
= \int_{-3}^3 \left[ \frac{1}{3}x^3 + x^2y + xy^2 \right]_{-1}^1 dy \end{displaymath}](img26.gif)
![\begin{displaymath}
= \int_{-3}^3 \left[ \left( \frac{1}{3} + y + y^2 \right) -
\left(-\frac{1}{3} +y - y^2\right) \right] dy \end{displaymath}](img27.gif)
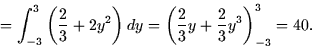



Next: Integration Over Non-Rectangular Regions
Up: Integration in Several Variables
Previous: Integration in Two Variablesby
Vector Calculus
8/20/1998
![]()
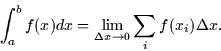
![]()
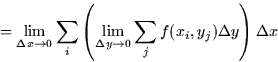
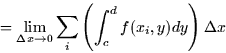
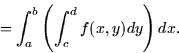
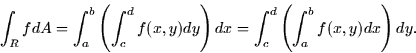
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()